0引言
国内外关于盾构施工在周围土层中产生超孔压的研究方法主要有现场实测、理论分析和数值模拟等。由于现场条件复杂,难以判断引起超孔压变化的主要原因以及各因素对超孔压变化的影响,且可能出现设备失灵的问题。如文献[2]对台北某隧道进行孔隙水压力测试,盾构机脱出时孔压计出现过短暂的失灵,盾构空隙产生的效果未捕捉到。此外,现有的实测资料仍较少;而现有的理论分析主要对模型进行简化,做出一定的假设,不能反映盾构施工过程的影响,目前用现有理论对超孔压进行较准确预测还有一定难度。由于盾构施工过程及超孔压的复杂性,目前已有的数值模拟结果与实际仍不太符合。这些模拟方法或者是忽略了盾构机、盾尾空隙和注浆压力的模拟,或者是对正面推力、注浆压力模拟不够准确,只是简单地以均布荷载表示,并且绝大多数模拟都没有考虑浆液性质的变化。
本文考虑盾构机、盾尾空隙的影响,并对正面推力和注浆进行精细化模拟,以探索更能符合盾构施工过程的超孔压数值模拟方法,并得到盾构施工引起的周边土体超孔压变化特性及规律。
1盾构施工的有限元模拟方法及可靠性验证
1.1模拟方法
利用Plaxis3D有限元软件中的biot固结理论计算超孔压的产生与消散,盾构机的施工过程模拟考虑了盾构机、正面推力的大小及分布方式、盾尾空隙、同步注浆浆液性质随时间的变化及分布方式等。
具体的模拟方法如下所述。盾构机采用实体盾壳单元模拟,将盾构机的重量折算到盾壳上,盾壳厚度为50mm,用各向同性的板单元模拟,重度γ=120kN/m3,弹性模量E=23×106kN/m2,盾构机直径为6340mm。千斤顶推力简化为均匀荷载作用在盾构机后方衬砌上,其值为2300kN/m2。
在盾构施工工程中,一般取土仓压力为施工控制参数,并认为土仓压力与正面推力是相等的。但根据长三角软土地区某盾构隧道的实测统计数据可知,土仓压力与理论计算的静止土压力比值为1.16~1.74,平均值为1.34。其从上到下为梯形分布作用在圆形开挖面上,如图1所示。
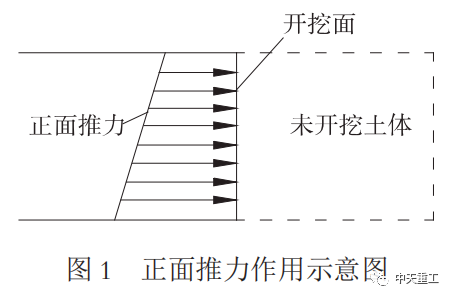
盾尾空隙大小一般为80~160mm[11]。由于软土中超挖量较小,认为盾尾空隙主要由盾构机壳厚度和盾尾操作空间决定。本文取盾尾空隙的厚度为70mm,用模量极小的弹性材料模拟,E=20kN/m2。
同时考虑浆液性质随时间的变化以及注浆压力的大小与分布。采用线弹性材料模拟单液活性浆液的性质变化,并根据对浆液的室内无侧向抗压试验和土工试验规范,拟合出浆液弹性模量随时间的变化函数作为有限元模拟值[12]。其拟合函数为

由于浆液最终凝固成混凝土,所以y值增大到混凝土的弹性模量时为止,之后保持不变。注浆层的厚度为70mm,分布于管片外侧。由文献关于注浆压力随时间变化的试验结果可知,当盾尾通过后,注浆压力会在较短时间内消散并达到均匀。随着浆液的凝固,注浆压力消失,浆液开始承受地层中的水土压力并传递到衬砌上。据此,确定本文有限元模拟中注浆压力的作用时间仅为盾尾脱出一环管片后的时间,随着盾构的向前推进,注浆压力随即消失。注浆压力的分布形式为沿深度呈梯形分布,沿深度不断增大。注浆压力与理论计算的静止土压力比值为0.8~1.1,注浆压力作用示意图如图2所示。此外,浆液的充填性、流动性等也会影响注浆压力的大小和分布,在此处视为理想条件,不做过多讨论。
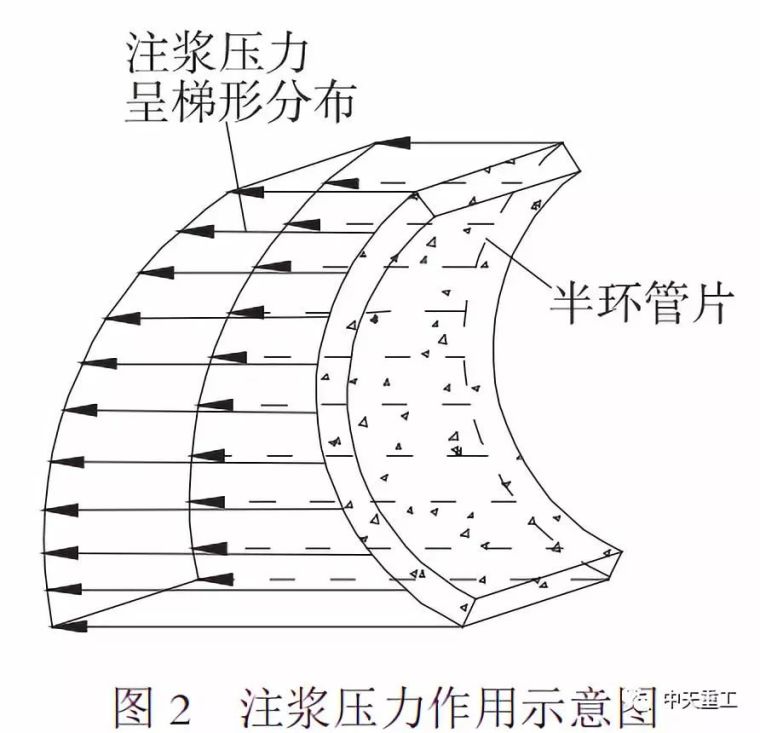
根据以上讨论,得到了盾构机、正面推力、盾尾空隙和同步注浆的模拟方法,由此可得到本文的模拟示意图,如图3所示。
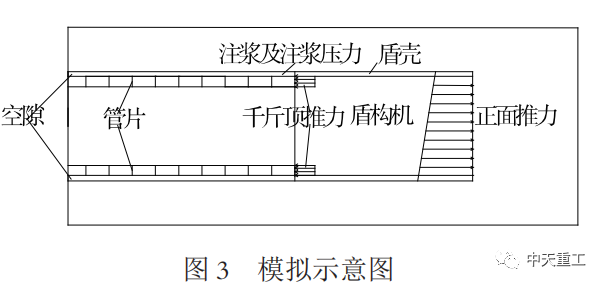
三维模型的边界条件是:四周表面和底面为法向位移约束,表面自由。开挖面边界条件如图3所示。渗流边界为表面透水边界,模型四周和底部为不透水边界,衬砌处为不透水边界。
1.2可靠性验证
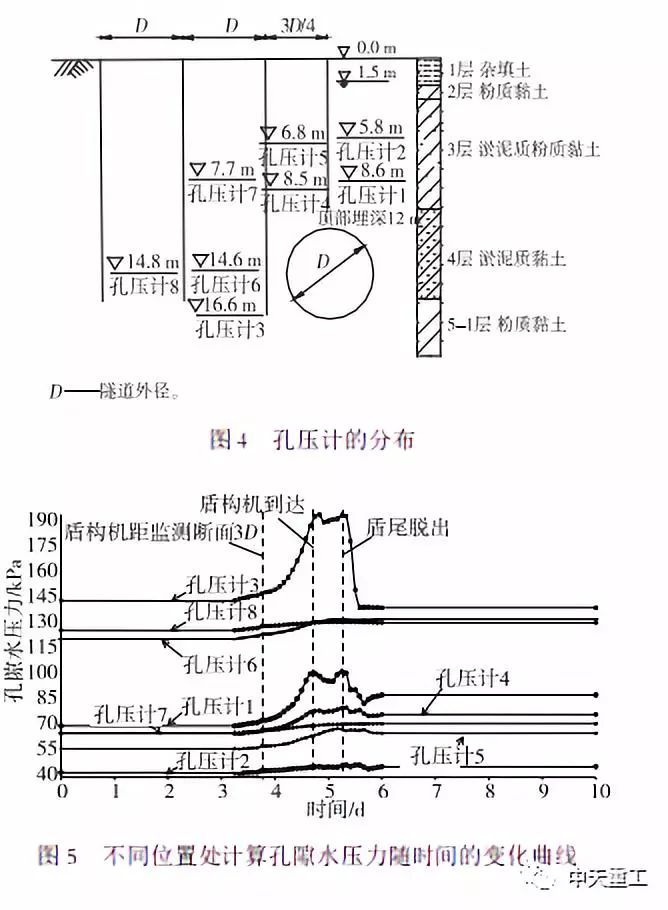
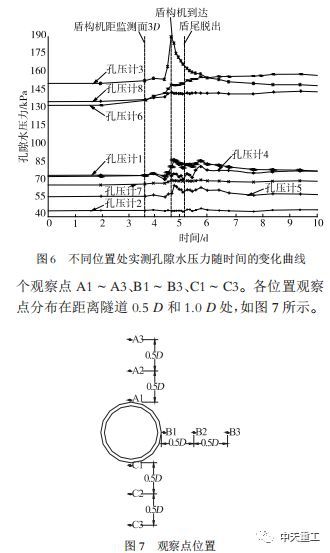
为了验证模拟方法的可靠性,根据上述有限元模拟方法,采用文献中的工程及参数,以实际工程为例建立模型,并与实测孔压值进行对比验证。文献中实测孔压计分布和地层情况如图4所示。计算值和实测值的对比,如图5和6所示。由图5和图6可知,各孔压计的初始值、稳定值以及变化趋势基本一致;孔隙水压力在盾构到达不同位置处会出现不同程度的突然增大,盾构离开后,孔隙水压力也开始衰减。但由于现场施工情况复杂多变,有限元模拟不可能完全准确模拟,所以在量值和变化趋势上会有一些差别,但整体规律是符合的。
2施工引起的周边土体超孔压分布特性
2.1模型参数
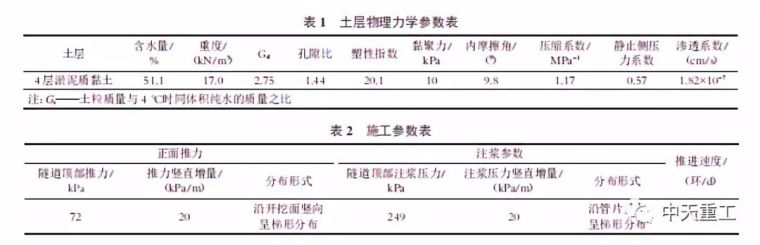
为减少土层非均质对超孔压变化规律的影响,此处选取盾构隧道位于单一软土层。计算中隧道顶部埋深12.4m,地下水位为地表以下2m,隧道管片外径6.2m、内径5.5m、宽1.2m,盾构机的直径为6.34m。所建立的有限元模型长80m,宽20m,高30m。土层物理力学参数如表1所示,施工参数见表2。
2.2计算结果
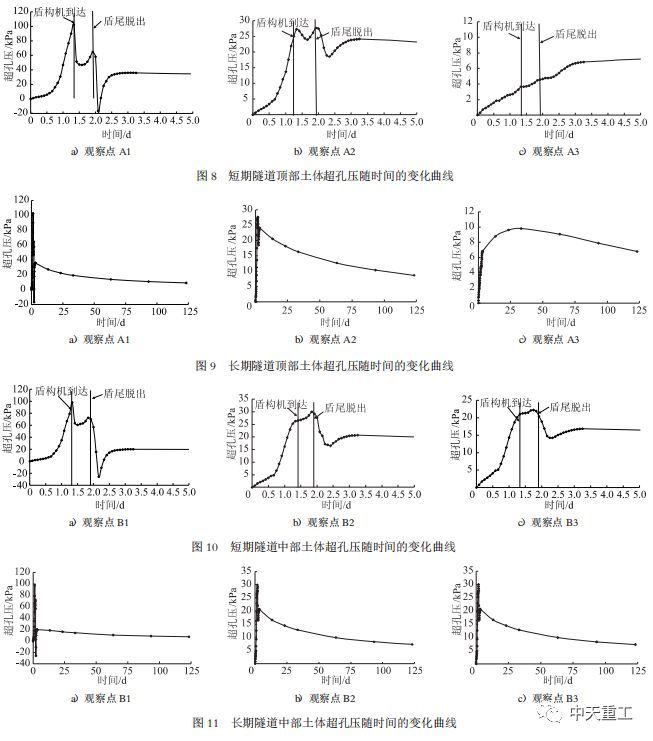
分别在隧道顶部、中部和底部各选取3个共9个观察点A1~A3、B1~B3、C1~C3。各位置观察点分布在距离隧道0.5D和1.0D处,如图7所示。
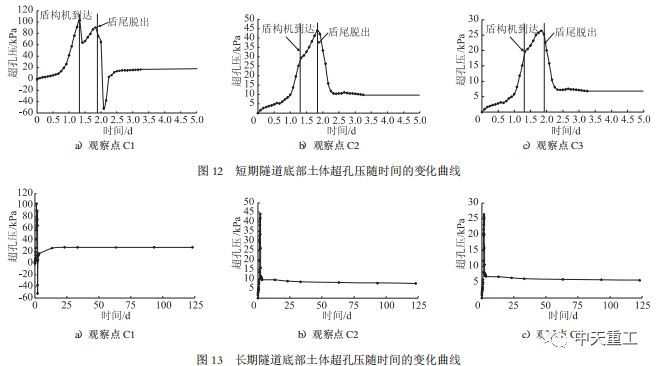
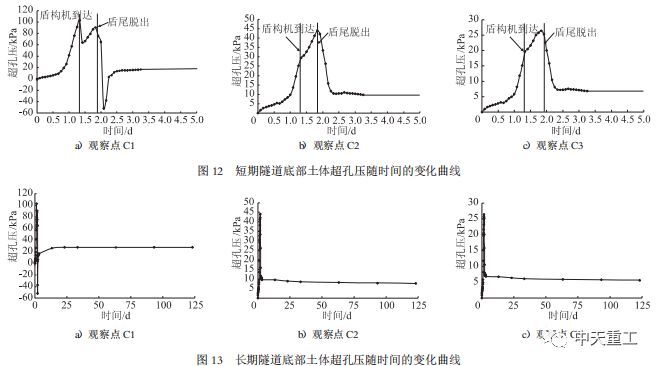
各观察点超孔压随时间的变化分别如图8~图13所示。每个观察点均给出了超孔压短期(5d)和长期(125d)的变化过程。由图8、图9可知,盾构施工中隧道顶部土体中最大超孔压为100kPa,发生在A1点。A1、A2两点超孔压随盾构施工过程的变化明显,A3点不明显。125d后A1、A2、A3点超孔压的衰减率分别为91%、68%和45%,说明距离隧道越近超孔压的变化幅度越大。
与顶部相比,隧道中部和底部超孔压规律相同,仅量值上有差别。如隧道中部最大超孔压为97kPa,而底部为103kPa。超孔压125d后B1、B2、B3点超孔压的衰减率分别为92%、76%和69%,而C1、C2、C3点超孔压的衰减率分别为92%、81%和78%。
综合以上隧道顶部、中部和底部超孔压随时间的变化可知:距离隧道越近,超孔压受盾构施工的影响就越大,在隧道周边位置,均会出现两次极值,分别在盾构机到达和盾尾脱出的时刻(分别定义为第一极值、第二极值),且第一极值明显大于第二极值。说明掌子面推力对隧道附近土体超孔压的影响比注浆的影响大;随着距离的增大,虽仍会出现两次极值,但两极值的差异不明显,甚至出现第二极值大于第一极值的情况,此现象的出现为超孔压的累积效应;随着距离的进一步加大,如大于1D的位置,盾构施工产生的超孔压不明显,超孔压的变化与盾构施工过程并无明显对应关系。
3结论
(1)计算结果与实测结果基本符合,说明本文的模拟方法可靠,可用于计算盾构隧道施工引起的周边土体超孔压。
(2)随着盾构机的推进,隧道周边土体超孔压逐渐增大,在盾构机到达和盾尾脱出注浆时会出现两次极值,隧道附近超孔压随施工过程的变化非常明显,第一极值明显大于第二极值;较远处差异不明显,甚至出现第二极值大于第一极值的情况;随着距离的进一步加大,如大于1D的位置,盾构施工产生的超孔压不明显,超孔压的变化与盾构施工过程并无明显对应关系。
(3)盾构机离开后,超孔压会缓慢消散,消散所需时间较长,在软土层中125d后隧道四周超孔压的衰减率约为92%。






