有些桥梁设计师或年轻桥梁工程师在使用有限元软件的初期,容易有一个潜意识里的错误认识,即认为有限元是一个精确的分析方法。
有限元是一个强有力的、有较高精度的数值方法,但并不是一个精确的方法。简单回顾一下有限元法理论,就能容易地知道这一点。下面以位移法有限元为例来说明。
有限元法是把连续的(具有无穷多个质点的)求解域划分为含有有限个子域(单元)的离散网格形式(见图2)。这些单元之间通过有限数量的网格节点相互连接,用这些离散的节点处的位移表征实际结构中连续的位移场。在这些节点上,位移是连续的,但位移的各阶导数并非都是连续的,取决于节点位移未知数中是否包含这些导数。这是有限元法的第一个近似之处。在单元内部,由于不知道真实的位移场函数,所以有限元法采用近似的数学表达式(如多项式)通过节点位移进行插值来描述,该表达式称为插值函数。这是第二个近似之处。在节点之间的连续边界上,位移及其各阶导数是否连续则取决于单元位移模式和插值函数的形式,一般最多使一阶导数连续。这是第三个近似之处。
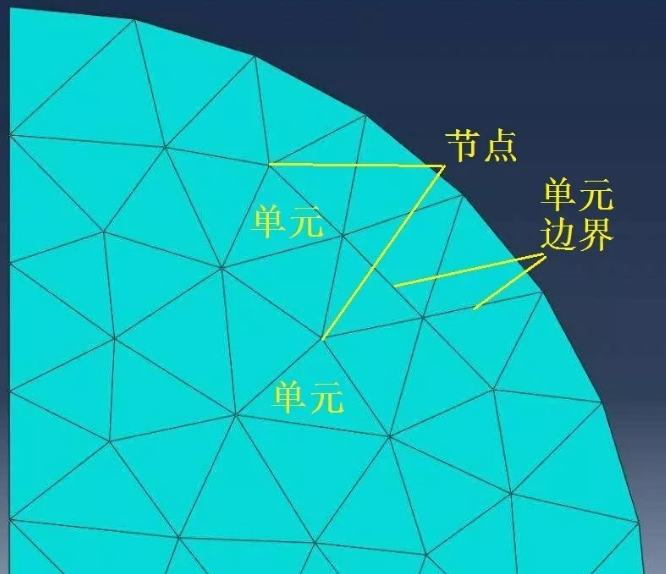
图2 有限元网格
在位移法有限元中,采用能量原理建立以节点位移为基本未知数的平衡方程组,所以求解有限元问题归结为求解一个大型线性方程组的问题(即使对于非线性问题,在进行每一迭代步或者增量步求解时,也是一个线性的方程组)。该线性方程组一般为式(1)所示的形式。其中[K]为方程组的系数矩阵,称为总刚度矩阵,{δ}为方程组的基本未知数,即结构的节点位移列向量,{P}为荷载列向量。方程组可能含有成千上万乃至几百万个未知数,那么由于计算机中数字的字长(通俗地说就是有效数字位数)是有限的,因此在求解过程的大量计算中,会由于舍入误差而产生计算误差,这是第四个近似之处。这些只是有限元法本身的近似之处,还不包括力学理论、模型与实际结构差异、计算参数与实际结构差异等引起的误差。
![]()
上面的描述虽然不太严谨,但已经能够清楚地看出,有限元法是一种近似的数值方法,是有误差的方法。






