当材料被拉断时,拉应力超过了材料分子原子间的化学键的引力而断裂。但压力会使材料分子、原子间的间距越来越紧密,所以理论上不存在材料被“压坏”这种情况,除非像黑洞那样的压力才可能把原子本身压塌缩。但很多的构件的确受到“压缩”而破坏,本质是材料找到了侧向逃脱的渠道而避免了过大的压缩荷载。混凝土的压溃,钢材的“压扁”本质都是形成侧向逃脱的剪应力的存在导致的。
从材料力学我们知道,水平面上的垂直应力会产生斜截面上的剪应力。当颗粒足够密时,继续增加的上部压力产生的某斜截面上的剪应力达到该截面的抗剪应力的时候,土体就会滑动,也就是我们常说的土体“失稳”。所以地基有两种破坏情况,一种是“失稳”,比如滑坡、基坑坍塌、地基极限承载力等本质上都属于这个。
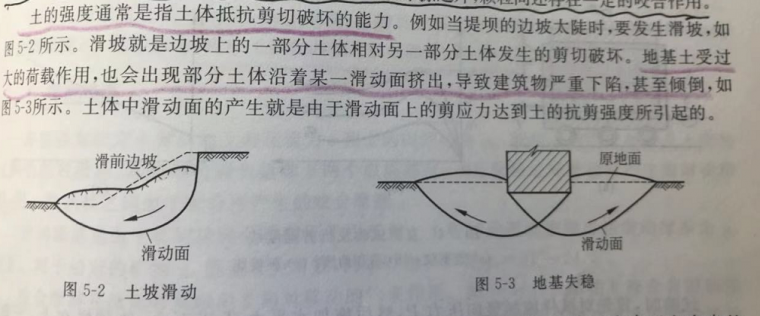
二是压缩变形即基础的沉降,其本质并不是地基土的破坏,而是土体压缩变形到一定程度(土体还可以承受压力的增加造成的土体变形,距离其局部剪切破坏仍有很大的富裕),上部结构无法承受了,即规范所谓的变形控制。
所以建筑地基结构地基基础既要保证不能“失稳”破坏,也要保证地基土的压缩变形不能超过结构允许的程度。看下图:
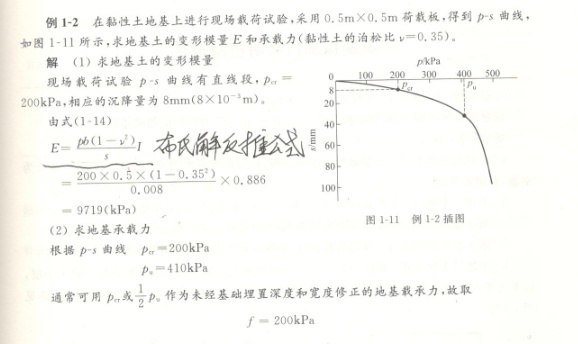
Pcr 代表的是土体仅仅压缩变形时的最大应力,对应的变形模量用来算建筑的沉降,这个距离土体的剪切破坏的失稳还有好远一段距离。Pcr后开始土体最大的剪应力处开始剪切破坏,即所谓的土体局部塑性,逐步发展,直到Pu时,剪切面连在一起形成整体滑切失稳破坏,叫极限稳定平衡状态,也即我们所谓的地基极限承载力。结构设计不能用这个极限承载力,太不安全了,所以一般用刚开始时候的那个承载力比Pcr稍微大一点。
本文拟谈谈地基土的“失稳”破坏问题,首先就是土的抗剪强度指标。
一:土的抗剪强度指标
无需多言,结构人都知道土的抗剪强度指标是黏聚力c和内摩擦角地基基础设计思考与实践—土的抗剪_4。
见下图:
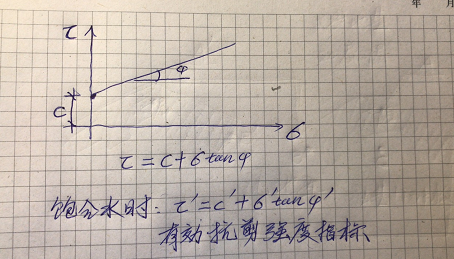
这就是著名的库伦公式。黏聚力c可以理解为土颗粒之间的复杂的电化学作用,地基基础设计思考与实践—土的抗剪_6更容易理解,就是土颗粒之间的咬合力,我们初中学到的摩擦系数。
有水的时候,情况就变了,这些参数都变小了。水在地基里面是一个非常重要的课题,本系列还未涉及,后文会专门描述。
砂土的地基基础设计思考与实践—土的抗剪_7一般比粘性土,大约为30~400,但c比粘性土小(约10KPa以内),粘性土地基基础设计思考与实践—土的抗剪_8一般为0~300,c从10KPa~200 KPa。
得到这些土的指标及保证准确性是非常不容易的事儿,是岩土工程的重要课题之一,结构师只需理解这些概念即可,以便正确的运用地勘给出的这些参数。
二:土的剪切破坏(极限平衡理论)
土中任何一点既有剪应力又有压应力,当该点的剪应力等于该点的抗剪应力时就是平衡状态。上文我们知道了土的抗剪应力的公式,那土中外荷载作用下的剪应力是多少呢?
这是材料力学的应力求解在地基中的应用,本无需讲的,但考虑很多工程师估计都忘的差不多了,我们概念上一块复习一下。
图中某处微单元受到到两对正应力和两对剪应力的平衡力作用,见下图(不考虑垂直纸面的方向),通过力的平衡方程总可以得到两个互相垂直的微单元面上只有两对正应力而没有剪应力,这两个正应力就叫主应力,知道了这个主应力的大小和方向,就可以用公式求出任何一对垂直面上的正应力和相应的剪应力,也可以用作图的方法很容易的求解,这就是莫尔应力圆。
见下图:
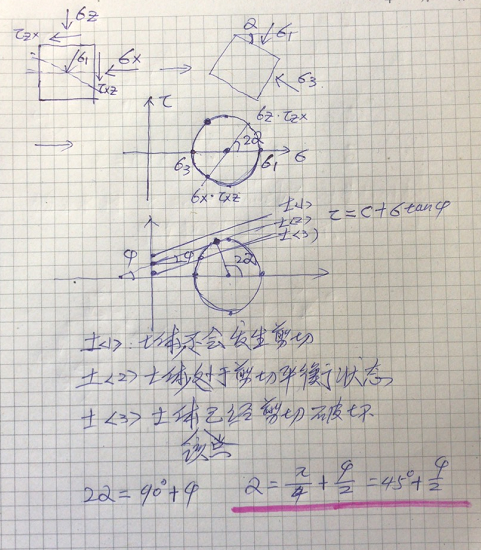
莫尔应力圆上的力是外力作用下的土体内部某点单元体某个角度面上的应力,而库伦公式斜线上的是正应力外力作用下的抗剪能力,所以抗剪能力关系斜线和莫尔圆的关系如上图,如果刚好如土<2>的相切就正好是剪切平衡状态。
注意,与主应力面角度为地基基础设计思考与实践—土的抗剪_10的应力在莫尔应力圆上直接量取2地基基础设计思考与实践—土的抗剪_11角度的圆上的点对应的坐标就是对应的该面上的正应力和剪切应力,这是几何作图很容易算出来的。
如果我们假设一个如下图的护坡,土自重产生垂直应力,护坡墙提供水平应力,这两个垂直面正好没有剪应力,可以当成主应力。那么该土体的滑切面与水平面的夹角就是地基基础设计思考与实践—土的抗剪_12
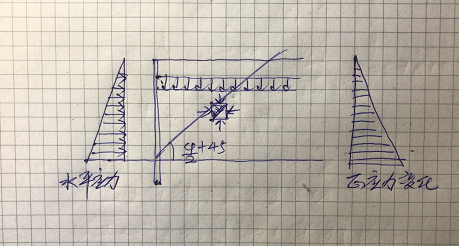
郎肯、库伦土压力理论、静止土压力系数等都和这个所谓的滑切面有关(下文另说)。
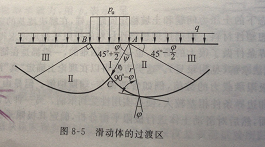
受到基础压力的地基土的极限承载力大小也和这个角度有关(下文另说),见下图:
三:挡土墙侧向土压力
1、静止土压力系数
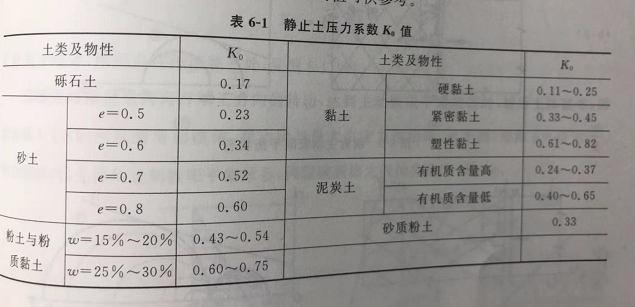
如果挡土墙刚性非常大,例如建筑地下室的外墙,土体没有任何位移,图中的剪应力远小于其抗剪应力,类似于材料弹性阶段。所以可以用泊松比算出,当然实际土体比较复杂,一般实验得出(见系列三),经验公式为地基基础设计思考与实践—土的抗剪_16,下图为常见图的地基基础设计思考与实践—土的抗剪_17。
2、主动土压力理论
当土体侧压力推动挡土墙向前运动时,土体沿地基基础设计思考与实践—土的抗剪_19滑切面向下维持平衡状态时,这个滑动土楔体对挡墙的推力,叫主动土压力。
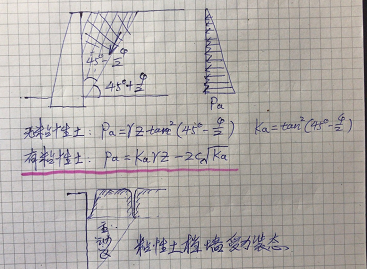
对于有粘性的土,粘聚力C表现为负压力,其值为常量不随深度变化。在土体上部自重应力较小处,会出现负值,但实际是没有负值的,只是土体和挡墙会脱开,见上图。
3、被动土压力
当墙推动土体产生向斜上的运动趋势达到滑切面的平衡状态时,墙体受到的土压力叫被动土压力,一般的建筑结构这种情况比较少见,比如推力拱桥的基础受到耳朵土压力。
注意这时土压力大于土垂直压力,侧压力为应力莫尔圆的那个大的主应力地基基础设计思考与实践—土的抗剪_21,所以滑切面与垂直面夹角为地基基础设计思考与实践—土的抗剪_22。见下图:
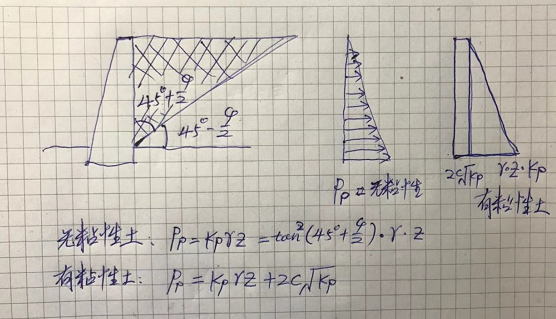
被动土压力也分两部分,摩擦力产生的和黏聚力产生的。
4、三种土压力的讨论
从上述分析可以看出几点:
(1)主动土压力系数地基基础设计思考与实践—土的抗剪_24<静止土压力系数< span="">地基基础设计思考与实践—土的抗剪_25<<被动土压力系数< span="">地基基础设计思考与实践—土的抗剪_26。压力的大小取决于挡土墙与土的相对位移,所以并不是一个常数。上述的三个地基基础设计思考与实践—土的抗剪_27只是三种特殊的情况而已。
有资料显示,中密的砂时档土墙的变形地基基础设计思考与实践—土的抗剪_28与土压力的关系如下图:
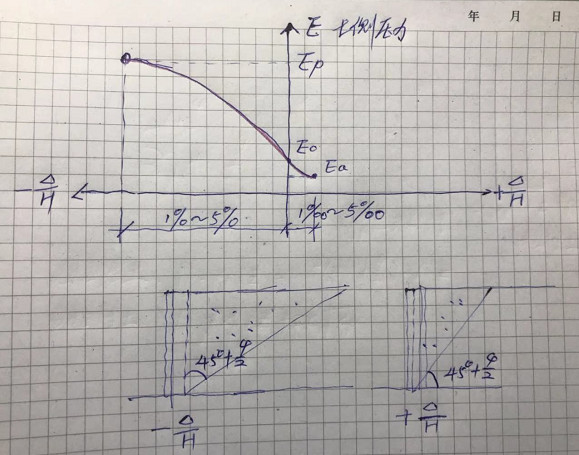
从图中可以看出,产生被动土压力那种平衡状态的难度比产生主动土压力时要难的多,其变形约为1/20~1/100,远远大于了建筑物或构筑物允许的变形,所以实际的建筑工程很难发生被动土压力,因为在发生被动土压力之前建筑已经破坏了。
地震下的建筑地下室有朝向土体移动的位移,可能造成被动土压力,从上述数据来看,这种相对土体的的推动的位移实际很小,一般地下室的位移约为1/5000,从上图看出,地震下的外墙土压力非常接近静止土压力,对于岩石等很硬的土体,因为岩石与外墙之间的防水保护等,实际的产生的土压力会小于静止土压力。所以在地震作用下的山地建筑的外墙考虑1.2倍的静止土压力安全度是足够的。
对于坡顶有建筑物或地面荷载时,静止土压力也包含坡顶有建筑物或存在地面荷载时产生的压力。
《山地建筑结构设计标准JGJ/T-472-2020》中对岩土对建筑外墙的力作如下规定:


《山地规范》地震下结构外墙的土压力的取值,被动土压力一定是太大了,弹性地震作用与静止土压力之和表述模糊,不如直接取静止土压力的1.2倍简单并且可靠。
(2)很容易判断,摩擦角越大、粘聚力越大,静止土压力和主动土压力越小。被动土压力正相反,不过我们很少用到,出现这种情况时要知道土越硬土压力越大。
(3)对于挡土墙的设计,结构工程师一般只能做比较矮的挡土墙,按静止土压力进行计算基本上满足要求,对于比较高的,情况比较复杂的,一般应该由岩土工程师进行设计。
上述均未涉及的水的影响,实际上其影响非常大,本系列拟专门另外论述。
四:土坡的稳定(滑坡)分析的简单概念
滑坡是岩土工程设计师的工作重点,是非常复杂的问题。结构工程师一般无法设计,但理解其概念也很重要。结构工程师对于一块山地的场地能够敏感的感觉到坡地的稳定性,以及当建筑位于坡顶时场地的稳定性都是非常重要的概念。理解这点可以很好的和岩土工程师去合作完成项目。
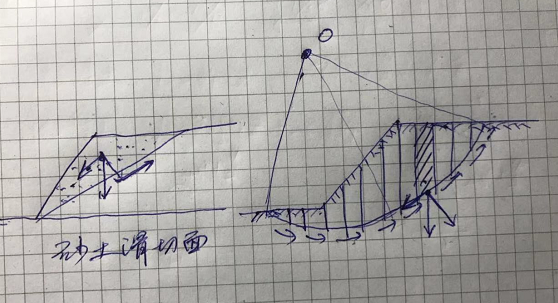
土坡的稳定本质上是一块土体沿斜面的滑动,也是剪切平衡的问题,和土体的摩擦角和粘聚力两个参数有关,和土坡本身的坡度关系也很大,与水的关系更大。土体的复杂性使确定滑动面变的很难。砂土的滑动一般是斜平面,所以砂土确定其滑切面相对容易,按滑动面上的土楔体的平衡进行计算。粘性土是一般是斜向的弧面,确定非常复杂,计算理论很多,主要是各种分条法,按沿弧面转动的平衡力矩进行平衡计算,结构工程师不需太关注。
五:地基承载力标准值及设计值的确定
本文开始已经说道,地基承载力是在地基压缩到一定程度,开始出现局部滑切破坏时的承载力叫临塑承载力,而极限承载力为滑切面形成整体时平衡的承载力。规范的地基承载力标准值一般是按极限承载力的1/2~1/3确定。但很软的土,几乎从一开始就伴随着压缩开始出现局部剪切即局部塑性变形,对这种承载力只好按某一较小的变形量来确定为地基承载力了。
建筑基础沉降的控制值一般要求是小于临塑荷载时的沉降。理论上变形计算满足了,地基承载力也自然满足,但是沉降计算比较复杂,不好控制,所以对重要的建筑两者一般都需要计算。
对于一般的要求不高的建筑,按上述原则确定的地基承载力设计的建筑其变形一般都在临塑荷载以前的阶段,变形主要是压缩变形,不会发生剪切的塑性变形(可以很小范围的塑性变形),承载力满足时,其沉降变形自然满足,所以地基承载力的确定暗含这变形的控制要求。
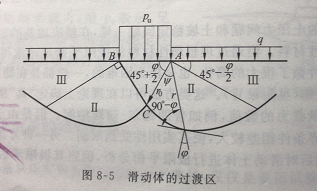
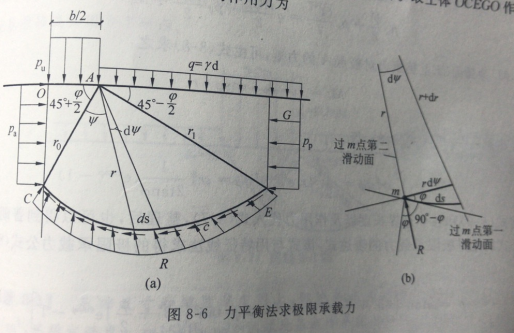
从上图可以看出,极限承载力和土体的抗剪指标黏聚力和内摩擦角以及基础地面以上一定范围(约2倍的基础宽度)的荷载(填土或建筑重量)有关。规范给出的未修正的承载力特征值是没有考虑地基顶面上部荷载的情况下得出的,所以应该根据实际情况进行修正。知道极限承载力来历的概念,就很容易理解规范的承载力修正的道理了。
(1)宽度修正系数是因为基础实际宽度带来地基土滑切面的比实测值或实验值的扩大带来的有利影响,故和基底以下的土的重量地基基础设计思考与实践—土的抗剪_35有关。而深度修正系数是基底越深,基底上部的荷载越大,所以和基底以上的土重地基基础设计思考与实践—土的抗剪_36有关 。当位于水位以下时,因为有效的荷载变小了(一部分荷载直接被水传到下面地层了)所以要采用浮重度。
(2)无论深度修正和宽度修正都和基底下土的抗剪特性有关,即土内摩擦角越大,粘聚力越大,即抗剪强度越大,修正系数越大。规范给出承载力修正表中的这种趋势是非常明显的。
(3)结构施工完成时,对于基坑没有回填时,地基承载力应该按未回填的地面计算,就很容易理解了。
(4)地规5.2.5直接利用地基的抗剪指标进行承载力计算,原理就是上面讲述的,规范的承载力调整系数相对于极限承载力的三个系数小的多,显然已经考虑了足够的安全度。但要注意,第一这个承载力不能进行修正,第二还要计算地基变形,第三是基础荷载偏心距不能超过0.033才能使用,所以实际工程中使用这个公式的很少。
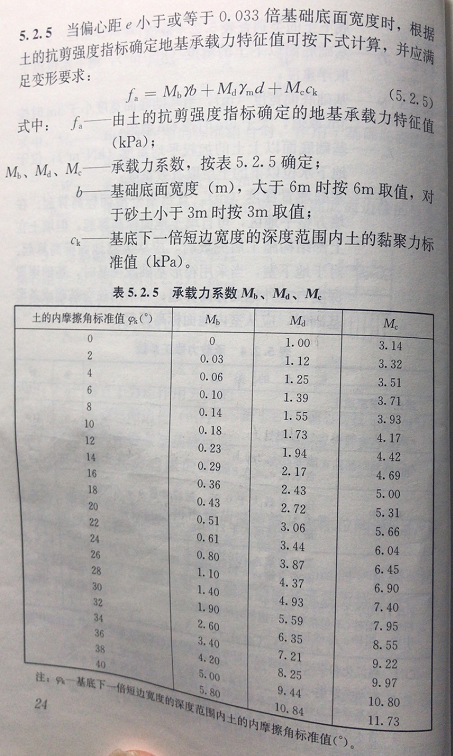
(5)岩石无需修正,是因为它太强大了,即使超高层的千米建筑也不足以使其整体滑动破坏,只能是有限的压缩,所以岩石用的是实验室的轴压强度乘以一个折减系数,是足够安全的。

本文只是简单的概念,以使结构师理解复杂的地基岩土概念,便于应用地勘的有关数据进行设计,同时对和建筑有关的岩土问题更方便与岩土工程师合作。而实际岩土的复杂性比本文论述的要复杂的多的多。






