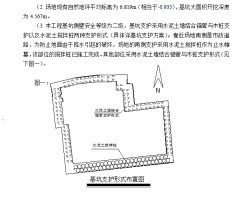
一、数值模拟对象
靖江凯旋国际广场基坑工程试验报告中的不可回收加劲桩JJ01,桩长18m,倾角30°,插件规格3×φ15.2,3个锚定板(也称分散板),其设计剖面图如下:
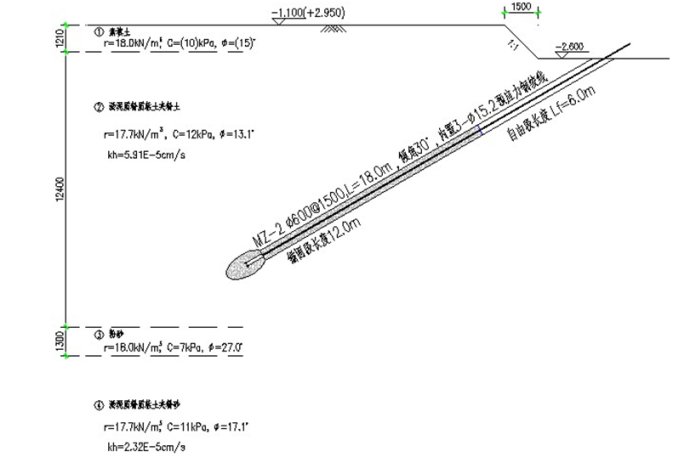
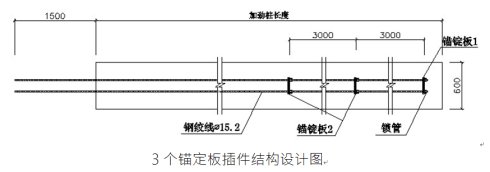
水泥土桩体直径D_pile=600,桩长pilelength=18000。钢绞线为3×φ15.2,直径d_shaft =45.6mm,长度等于桩长,其中分为自由段6000和锚固段12000。锚固段埋置了3块分散板,直径d_plate =200,由浅到深分散板编号为1、2、3,距离锚固段顶的距离分别为6000、9000、12000。
二、ANSYS数值模型介绍
1、模型基本尺寸和参数
为了简化分析过程,将上述斜向支护桩近似为竖向抗拔桩,竖向抗拔桩即可简化为2D平面轴对称模型,模型中建立了钢绞线杆轴、水泥土桩体和土体的实体单元,单元类型为PLANE42。假设分散板刚度无穷大,分散板与上下水泥土完全粘结,即分散板处水泥土的竖向位移与分散板及连接的杆轴节点位移相同,模型中没有建立分散板,通过耦合水泥土与同样深度的杆轴节点位移来实现。杆轴-水泥土桩体、水泥土桩体-土体之间建立了粘结滑移单元(用法向和切向COMBIN39模拟),水泥土桩底部-土体建立了法向连接弹簧COMBIN39。钢绞线杆轴PLANE42单元为完全弹性材料,直径d_shaft =45.6mm(周长相同,侧摩阻力近似),等效弹性模量EX=0.511e5MPA(保证轴向应变和伸长量相等),土体PLANE42单元为理想弹塑性DP材料,土体弹性模量为11.2MPA,泊松比0.4,粘聚力为12KPA,摩擦角为13.1。
2、模型基本假定
1)分散板为刚度无穷大的刚体,分散板处水泥土的竖向位移与分散板及连接的杆轴节点位移相同;
2)水泥土桩体-土体之间处于无滑移的粘结状态;
3)水泥土桩底部与土体仅建立了法向连接,忽略切向连接;
4)考虑了杆轴-水泥土桩体之间粘结粘结退化效应。
三、ANSYS水泥土弹性本构关系数值模型计算结果
1、参数设置(2D规则plane42jingjiangpile20160403.txt),杆轴-水泥土桩体之间粘结-滑移关系为三线段五阶段模型,考虑粘结退化,分为弹性、弹性-软化、弹性-软化-退化、软化-退化及退化等五阶段。具体计算结果详见博文“ANSYS中2D应力分散型抗拔锚桩粘结应力是否退化对受力性能的影响分析”http://blog.sina.com.cn/s/blog_9f5beef70102x1hk.html
四、ANSYS水泥土弹塑性DP本构关系数值模型计算结果
1、参数设置(2D规则plane42jingjiangpile20160404.txt、2D规则plane42jingjiangpile201604041.txt),其他同上述模型,主要区别有2点,第一点是水泥土本构关系不同,0404.txt、04041.txt模型为DP本构关系,粘聚力为350KPA,摩擦角为31.9,膨胀角为0。第二点是收敛标准不同, 04041.txt的收敛标准为CNVTOL,F, ,0.01,2, ,而0404.txt、0403.txt的收敛标准为默认收敛标准。
2、计算过程中的收敛情况记录
模型0404.txt在默认收敛标准下的收敛情况如下,仅能在T=1.0386处收敛。
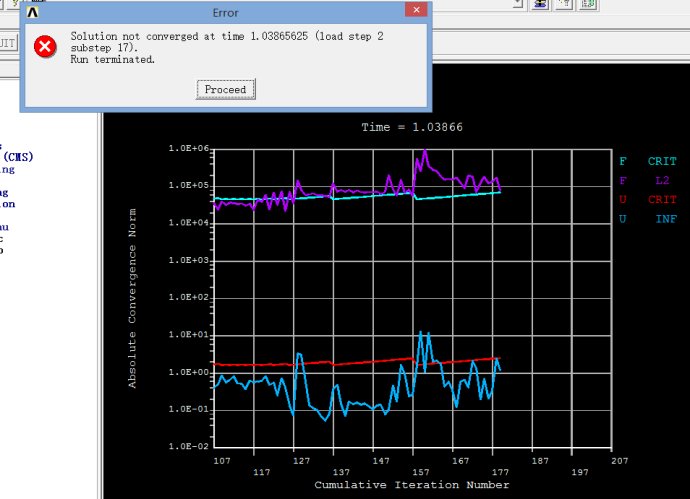
模型04041.txt在放松收敛标准下的收敛情况如下,仅能在T=1.0521处收敛。
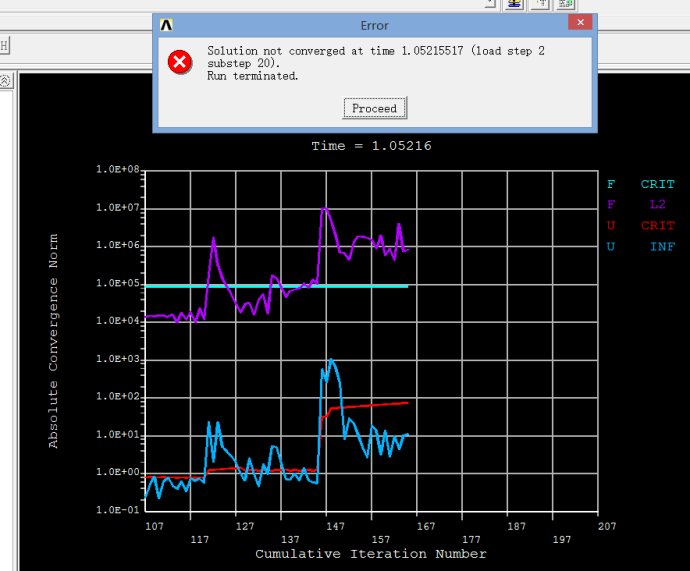
3、钢绞线顶荷载-位移曲线
模型0404.txt的荷载-位移曲线如下:
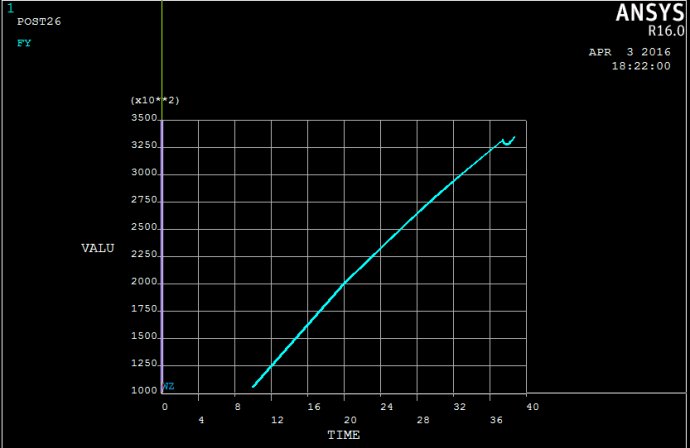
TIME FY
1.0100 105936.
1.0200 200559.
1.0268 254896.
1.0298 278147.
1.0328 300384.
1.0374 331614. (极限荷载)
1.0375 328943.
1.0376 328422.
1.0377 327789.
1.0380 327699.
1.0381 328185.
1.0382 329190.
1.0383 330209.
1.0384 331148.
1.0385 332163.
1.0386 333147.
模型04041.txt的荷载-位移曲线如下:
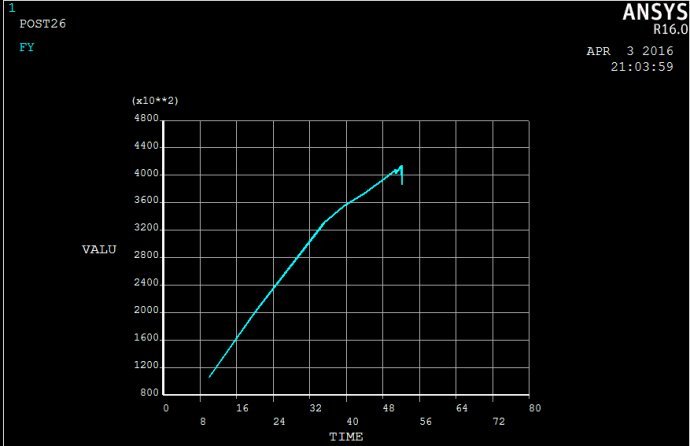
TIME FY
1.0100 105936.
1.0200 200559.
1.0350 329588.
1.0395 355247.
1.0439 373392.
1.0484 395516.
1.0508 408120.
1.0509 402918.
1.0510 404083.
1.0511 405512.
1.0513 406899.
1.0514 407826.
1.0515 408715.
1.0516 409667.
1.0517 410547.
1.0518 411488.
1.0519 412437.
1.0520 413198.
1.0521 413660. (极限荷载)
4、模型04041.txt的不正常计算结果
1)在T=1.0521时的土体竖向位移图中,桩底正下方的土体产生向下的位移有点不正常。同样的模型,当材料全部为弹性材料(2D规则plane42jingjiangpile201604042.txt)时,在达到极限荷载之前,该处土体的位移为向上。但有些水泥土弹性模型在过了极限荷载之后,该部位的土体位移也有向下的情况出现,说明水泥土本构改为DP并不是引起该异常现象的主要原因。我估计产生的原因是极限荷载之后模型的数值计算原因。
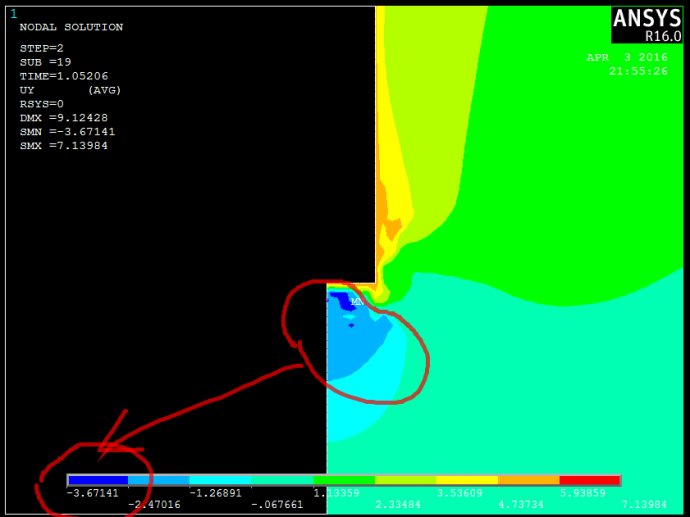
2)在T=1.0521时的土体剪应力TXY图中,桩侧土体剪应力数值过大,远大于土体的抗剪强度值。同样的模型,当材料全部为弹性材料(2D规则plane42jingjiangpile201604042.txt)、桩顶作用1000mm位移时,桩侧土体剪应力最大值仅为0.05MPA。但要注意,同样的剪应力分布图,ANSYS有时云图和路径显示的数值相差很大。
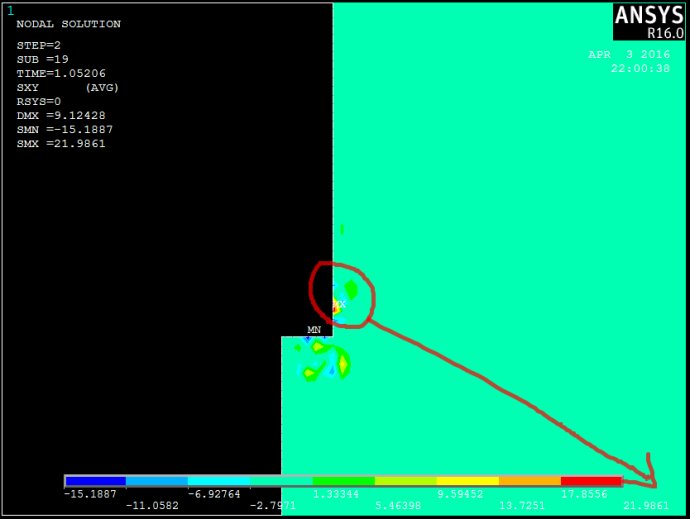
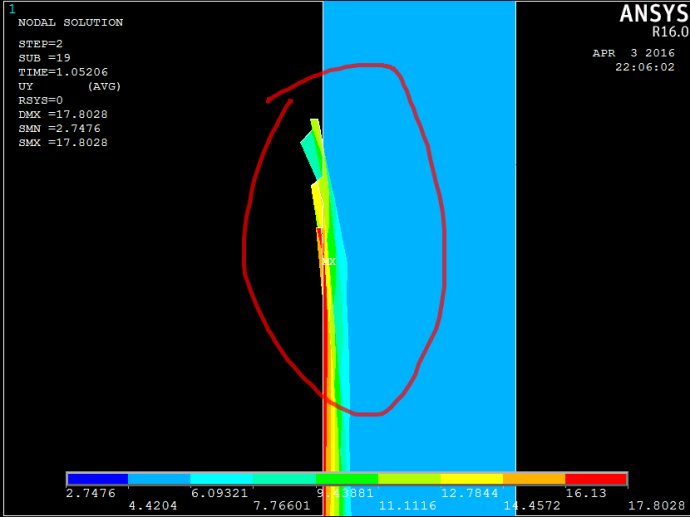
3)在T=1.0521时的桩体竖向位移图中,桩体中部竖向位移数值过大。同样的模型,当材料全部为弹性材料(2D规则plane42jingjiangpile201604042.txt)、桩顶作用1000mm位移时,桩体中部竖向位移较为协调。
五、对比结论
在数值模拟时,并不是考虑的因素越多,模型越复杂,其计算结果就越符合实际。有时适当简化模型,其计算结果更合理。以本次模拟为例,水泥土本构关系按弹塑性DP考虑,计算结果有很多失真之处。通过本例,我觉得,水泥土本构为弹性或DP,差别不大。