1 概 述
北京新保利大厦二期工程的正立面采用含主次索的复杂单层索网预应力玻璃幕墙体系,高90m,宽70m,面积之大堪称世界第一,效果图见文献[1]的图9。结合晶艺公司设计的此工程索网幕墙结构方案,在清华大学结构工程实验室内根据实际工程设计了1∶10的试验模型,并进行了8·6m×5·5m单层索网点支式玻璃幕墙的模型试验。单层索网玻璃幕墙被两根斜主索分成3部分:水平索主要承受风载,竖向索主要承受墙面自重,索网的两端固定在刚架边框上。本文结合此试验模型,介绍有限元程序的设计计算过程以及预应力的控制技术,为实际工程施工提供参考和依据。
2 模型的设计与分析
2·1 计算软件及有限元模型的选取
本项目在进行有限元设计分析时,采用目前在国际上得到广泛应用的大型有限元分析计算软件ANSYS,计算采用弹性-大变形有限元分析模块模型中幕墙拉索采用link10单元,该单元为三维只拉单元,用于描述拉索不能承受压力的特性,连杆采用link8单元,既可受拉也可受压。张拉过程中索的变形与拉力影响很大,因此在分析过程中考虑索的几何非线性。在模型承载过程中,索网的节点看作是铰接的;在模型张拉过程中,横索和竖索的节点认为在水平x方向和竖直z方向可以相对滑动,因此在ANSYS中把横索和竖索在y方向耦合起来,并通过对索施加初始预应变来模拟其预拉力。
2·2 基本参数取值及荷载计算
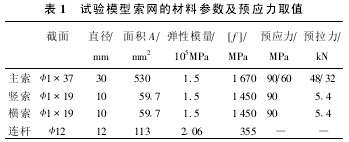
参考北京新保利大厦的实际工程,利用有限元软件反复设计和计算,保证索在施加预应力后在各种荷载组合作用下不发生过大变形或索拉力,结合实验室的条件,确定试验模型的材料参数取值见表1。试验模型的索网结构布置如图1,试验中对横索和竖索在每一步张拉时进行监测。
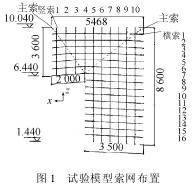
与试验模型采用的材料参数相对应的荷载结构自重为:墙面玻璃(采用6mm钢化玻璃)0·15kN/m2连接件0·11kN/m2,支承结构0·02kN/m2,合计墙面0·28kN/m2。风载:北京基本风压为wo50=45kN/m2(50年一遇)。《建筑结构荷载规范》(GB50009-2001)规定需计算围护结构的局部体形系数:正压区(迎风墙面+0·8,负压区(背风墙面)-1·0;封闭建筑内表面风压体形系数:正压区-0·2,负压区+0·2。C类地面粗糙度 0m高处阵风系数βgz=2·10,μz=0·74。地震:北京抗震设防烈度8度(第一组),设计基本地震加速度0·2g,水平地震作用地震影响系数αmax=0·16。索预拉力的原则是保证在各种荷载组合作用下不发生过大变形或过大索拉力,经有限元计算并考虑到试验条件,试验模型的主次索预应力取值如表1。
2·3 承载力及变形计算
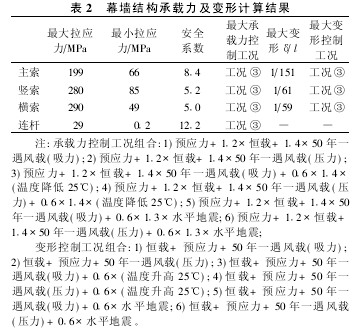
幕墙结构承载力及变形计算结果如表2所示。对于柔性结构,有关幕墙变形控制指标规范未规定。由于本工程单层索网结构的特殊性,不应采用现行规范衡量此工程平面内的变形性能(《玻璃幕墙技术规程》(CECS127∶2001)规定支承结构的相对挠度不应大于1/300)。从点支式玻璃面对变形的适应能力来考虑,在最不利荷载组合下,幕墙结构的变形可控制在1/50。表2中索网幕墙的变形满足这一要求。
3 预应力控制技术与分析
3·1 张拉方案的选取
在研究张拉力方案时,如果对所有索采用同步张拉,这样的设备及人力投入显然不可能。按传统方法在施工张拉时每一阶段张拉、每根索的张拉力均保持相同,由于索力相互影响,则张拉完毕后只有最后一根索力是设计值,此后要对前面所有的索进行调整,且每对索的调整量又不相同,同时调整的索力又对其他索产生影响。虽然从理论上分析,经多次反复张拉能使索力达到设计精度,但这样工作量将大大增加。此试验中采取倒拆法,考虑索之间的相互影响,运用程序调整到设计张拉值,然后进行倒拆(放松索),计算出在一次张拉到位时索的张力值。这样当张拉完最后一根索时,之前的索均能达到预定的索力值。
3·2 倒拆法有限元分析结果
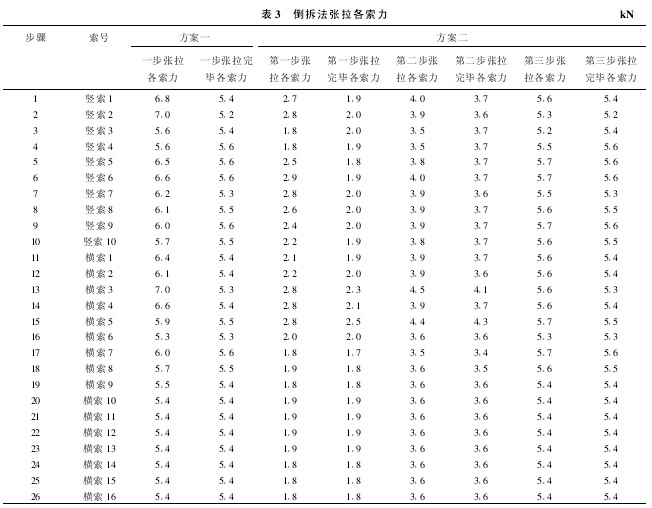
方案一:一步张拉到位。先张拉2根主索分别至48、32kN,然后依次张拉竖索和横索,所有横索和竖索只张拉一次,采用倒拆法进行有限元计算分析得出张拉索力,张拉过程及结果见表3。这种张拉方式在本试验模型中可以实现,但在实际工程中,可能因为张拉过程会对主体结构产生过大的局部应力而不能完成。
方案二:分三步张拉。先张拉2根主索分别至48、32kN,然后横索和竖索按照设计张拉力的33%、66%、100%的三阶段进行张拉,张拉过程及结果见表3,最终结果满足横索和竖索预应力90MPa左右在试验每一步张拉过程中,监测模型索力的变化,以便与有限元计算的结果进行比较。图2反映了ANSYS有限元计算中4根典型的竖索和横索在分三步预应力张拉全程中的应力变化。
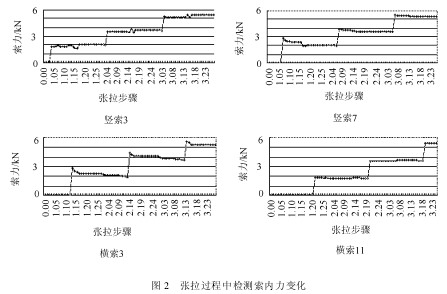
由计算结果可以看出:
1)一步张拉到位张拉次数较少,但是张拉过程中每根索需要张拉的力较大,而且由于索之间的相互影响,各索张拉的力差别较大,给施工带来不便。由于各索受力不均匀,张拉过程中作用在边框的力比较大,这在实际工程中可能会损坏周围的刚性边框。分三步张拉次数较多,但是张拉过程中各横索和各竖索之间的张拉力差别较小,特别是第三次张拉,各索力比较均匀,对边框的影响也比较小。
2)由于本工程模型含有主次索、横索和竖索组成三个平面,横索和竖索之间的相互影响较大,张拉过程中索力变化复杂,特别是索网上部横竖索之间影响很大。对于索网下部,从计算结果可以看出,对前面索力的影响很小。 4 结 论
1)由于索网体系分阶段张拉索之间的相互影响,采用传统的按比例等量加载顺序法施工,显然不如分级不等量加载的倒拆法施工。
2)借助有限元分析软件,对含主次索的复杂索网体系张拉及相互影响可以用计算机进行模拟分析,找出合理张拉顺序及张拉力的大小,为工程张拉过程提供依据。利用ANSYS软件对索网幕墙结构承载力及变形进行计算,可以选取恰当的材料参数和预应力值。
3)索网周围边框的刚度也是影响张拉阶段时各索力的因素,在本试验中经过加固后,边框的刚度很大,因此在分析过程中,不考虑边框的变形对索力的影响。
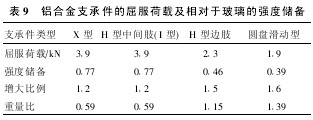
可以算出增大比例及增大后铝合金材料支承件与原合金钢材料支承件的重量比(表9)。计算结果表明,在保证支承件承载力的前提下,当采用铝合金材料时,X型支承件和H型支承件中间肢的重量减小,但H型边肢和圆盘滑动型支承件的重量增加。因此在工程中,X型支承件和H型支承件中间肢可以采用铝合金材料,而H型边肢和圆盘滑动型支承件采用铝合金材料则不经济。
5 总 结
本文在线性有限元分析的基|考试大|础上,给出了点式支承玻璃建筑中金属紧固件和支承件的承载力简化计算公式和优化方法,得到了以下结论:
1)传统弹性理论计算方法与试验和有限元分析结果相差较大,连接件的设计不能依据传统的弹性理论方法,应采用基于有限元分析和试验结果的简化设计方法。
2)在满足建筑美学和玻璃板孔径要求的前提下,支承件和紧固件的外形可以进一步优化,可以通过等比例缩小的方法减小连接件的尺寸,减少材料用量。3)紧固件和部分支承件也可以采用铝合金材料制造,由于铝合金材料重量比合金钢轻,因此可以降低连接件的重量和造价。






