城市经济基础理论中关于区分城市经济活动的基本和非基本部分的观念是简单明瞭的,但要具体区分却不容易。下面按发展顺序介绍几种有代表性的方法。
(一)普查法
通过发调查表和现场访问获得每一个企业和单位基本和非基本活动的信息,最后都折合成职工数,进而得到整个城市的B/N比。这一方法虽然可以得到比较准确的结果,但整个调查过程非常繁琐、冗长和乏味。当城市规模较大时,工作量浩瀚异常。如果想同时对比研究几个城市,简直就无法靠个人的力量得到第一手资料。
(二)残差法
这是霍伊特为了简化直接调查的程序而提出的一种间接方法。他先把已经知道的以外地消费和服务占绝对优势的部门,作为基本部分先分出来,不再过细的区分内部可能包含的非基本部分。然后从基本活动不占绝对优势的部门职工中,减去一个假设的必须满足当地人口需要的部分,霍伊特具体假设这部分职工中基本和非基本的比例为1:1。例如一城市有100000劳动力,其中20 000名明显属于以基本活动占绝对优势的部门,那末余下的80 000名按假设对半分为基本部分和非基本部分。这样,这个城市的B/N比为60 000:40000=1:0.7。这一方法的缺点是比较粗略,1:1的假设比率是主观确定的。
中国城市规划在调查基本人口时,为了简化过程也曾采用过这一方法。不过为了比较准确起见,常常是分别和有关的主管部门,共同讨论估计出每个部门的合适比例。①
(三)区位商法(也称宏观法)
这个方法的实质是认为全国行业的部门结构是满足全国人口需要的结构,因此各个城市必须有类似的劳动力行业结构才能满足当地的需要。低于这一比重的部门,城市需从外地输入产品或取得服务。当城市某部门比重大于全国比重时,认为此部门除满足本市需要外还存在基本活动部分。大于全国比重的差额即该部门基本活动部分的比重,把各个部门和全国平均比重的正差额累加,就是城市总的基本部分。
马蒂拉(J.M.Mattila)和汤普森(W.R Thompson)首先提出这种方法,②其数学表达式为:
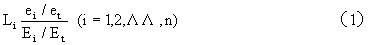
式中
ei——城市中i部门职工人数;
et——城市中总职工数;
Ei——全国i部门职工人数;
Et——全国总职工数;
Li——区位商。Ls大于1的部门是具有基本活动部分的部门。

(2)式中Bi为剩余职工指数。当Bi小于0时,i部门只为本地服务;当Bi大于0时,Bi就为i部门从事基本活动的职工数。

式中
B——城市中从事基本活动的总职工数。
区位商法大大简化了区分城市基本和非基本部分的复杂过程。适宜于对若干个数量不多的城市进行经济结构的对比研究。对大城市按中等尺度进行部门分类的对比研究效果较好。这一方法也可推广到省区级地域单元的城镇研究,用省区的平均结构作为标准来揭示省区内各城镇的经济基础的差异。
但是,区位商法的假设只有在国家没有外贸出口和全国各城市都有相同的生产率和消费结构的前提下才能成立。对于重要的出口部门,用全国比重去衡量城市满足本地需要的部分,显然标准就偏高了。城市之间在同一部门生产率的实际差别和消费习惯的不同也会影响计算的准确性。一些更尖锐的批评者认为,全国平均比重是一个非常容易变动的数,但大多数城市的经济结构,并不会随着全国平均数的变化而发生变化。而且全国的平均百分比数,从理论观点来看,是一个很难解释的统计学上的抽象。对并不是每个城市都可能有的所谓“散在部门”尤其如此。
(四)正常城市法
瑞典地理学家阿历克山德森在评价区位商法时,举例道:美国汽车工业职工占全国的1.5%,但只有12%的城市能有这么高的比例,最高的底特律为28%,而70%的城市只有0.2%甚至更少。因此1.5%的全国平均比重很不确切。为此,阿历克山德森在1956年研究美国城市经济结构时企图为各部门寻找一个“正常城市”作为衡量所有城市应有的非基本部分的标准。低于这一标准的部门,只为本地服务,在这标准以上的部分,是城市的基本活动部分。①
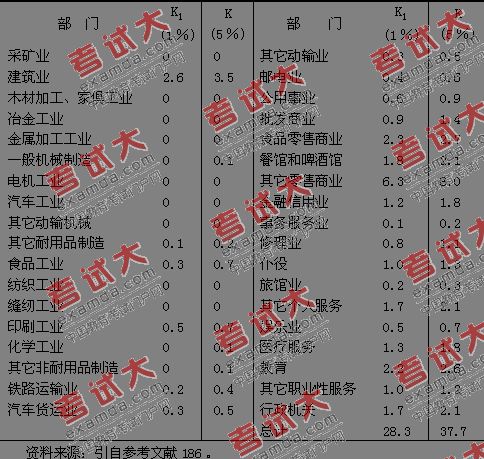
阿历克山德森收集了美国864个10000人以上城市的职工资料,按36个部门计算了每个城市的职工构成百分比。分别把每个部门的864个城市按职工比重从小到大排列起来,并据此画成各部门职工百分比的累积分布图。他经过大量的对比,最后确定选取各部门序列中第5个百分位(即第43位)城市的职工比重作为该部门满足本地需要的正常比重,并称之为K值。超出K值的部分为基本活动部分。
举例来说,图33a是美国城市批发业职工比重的累积分布曲线。在864个城市中,批发业比重最低的城市为0.01%,第2位是0.2%,……,第43位是1.4%,……,第863位是16.9%,最高的一个是18.7%。阿历克山德森即把K值定为1.4%,第43位以后的城市,批发业都具有为市外服务的作用,大于K值的部分即该市批发业的基本活动部分。
不是所有部门都象批发业那样存在于所有城市。有20%以上的城市就没有采矿业,这时K值等于0.0(图33b)。
36个部门的K值加起来一共是37.7%(表28)。意味着美国城市当时为本市服务的“正常的”职工比重应该在37.7%左右,即B/N比约为1:0.6。
阿历克山德森在大量的城市中寻找一个所谓“正常城市”的思想颇有新意。然而,尽管他在研究中曾尝试使K值分别取用第一个百分位(即第七个城市)和第五个百分位城市的职工比重(表28),经过大量对比,最后选用了第五个百分位,但这仍然带有较大的主观性,很大程度上是经验性的决定。在实际上,接近于作者想象中
表28 阿历克山德森对36个部门所取的K值
的具有37.7%非基本部分的所谓“标准结构”的城市,如罗得岛州的维索凯特,宾夕法尼亚州的塔摩库瓦,北卡罗来纳州的托马斯维尔等,都是人口仅1~5万的小城市。连他本人也为此提出疑问,这样选择出来的K值是否适合于内部交换比小城市大得多的较大的城市。
莫里塞特(I.Morrisset)1958年在阿历克山德森研究的基础上继续进行工作,从原来864个城市中删去了123个部门结构比较特殊的城市,余下的741个城市再分成美国东北部和西部南部两个地区,又把每个地区中所包括的城市分成7个规模组,分别找出了36个部门每个规模组城市的K值。分析得到了两个重要结果:①
表29 美国各部门职工比重、阿历克山德森的K值
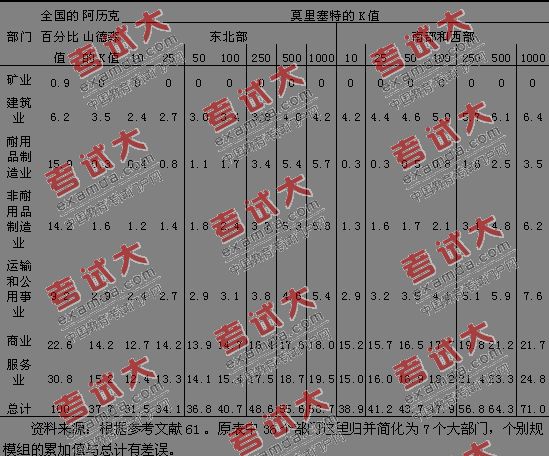
和莫里塞特的K值比较
(1)K值在经济发展水平不同的地区是有差别的。经济发展较早,制造业高度专门化的美国东北部城市,除了制造业以外,其它部门的非基本部分的比重(K值)都比发展历史相对较晚、城市密度相对较小的南部和西部要低;
(2)各部门的K值以及K值的和,无论在美国东北部或南部西部地区,都随着城市规模级的上升而提高,进一步证实了随着城市规模的增加,城市的非基本部分一般也相应增加。这也就说明,阿历克山德森对864个从1万人到数百万人的庞大城市体系,统统使用第五个百分位的“正常城市”作为标准划分基本/非基本活动仍有缺陷(表29)。
(五)最小需要量法
1960年乌尔曼(E.L.Ullman)和达西(M.F.Dacey)提出了另一种划分基本/非基本部分的方法,叫最小需要量法。它和区位商法、正常城市法的不同在于:①他们认为城市经济的存在对各部门的需要有一个最小劳动力的比例,这个比例近似于城市本身的服务需求,一个城市超过这个最小需要比例的部分近似于城市的基本部分;②把城市分成规模组,分别找出每一规模组城市中各部门的最小职工比重,以这个比重值作为这一规模组所有城市对该部门的最小需要量。一城市某部门实际职工比重与最小需要量之间的差,即城市的基本活动部分,把城市各部门的基本部分加起来,得到整个城市的基本部分。
用最小需要量法分析美国城市的经济基础,同样证实了城市的非基本部分随着城市规模的扩大而提高(表30)。
乌尔曼和达西分城市规模组来确定城市经济的基本/非基本部分,又向前跨出了一步,但仍不是尽善尽美。批评主要集中在两个方面。
首先,假如被选择出来作为衡量某一规模组最小需要量的那个城市,经济结构恰恰很特殊,不能代表一般状况,那就会影响一大片城市的计算的准确性。乌尔曼和达西的研究只把美国城市分成6个规模组,规模间也不连续,每个规模组只随机选择38个城市(100万人以上级为24个样本)。由于种种原因,的确使某些所选城市的代表性受到怀疑。例如首都华盛顿特别低的耐用品制造业和批发业比重被选作100万以上城市的最小需要量指标就是最突出的例子(见表30)。
表30 美国14个部门不同规模组城市的最小需要量(%)
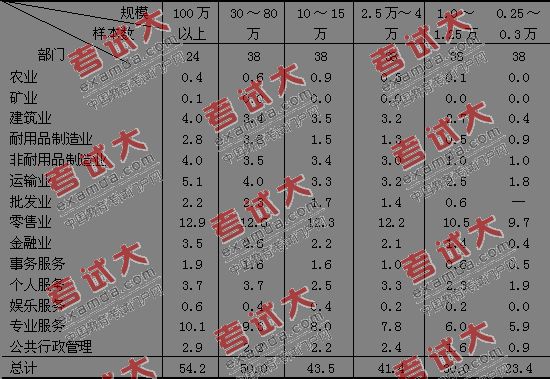
另一种更尖锐的批评认为,假如按照乌尔曼等的方法认为具有最小需要量比例的城市能满足自身需要,其余城市都有输出,那么就会得出一个矛盾的结论:几乎所有的城市都有输出,却没有一个城市需要输入。这一点也许正是最小需要量法与区位商法、正常城市法相比,在理论上的一个漏洞。批评者半认真半开玩笑地说:不是所有高于最小需要量的城市输出货物或服务,而是所有高于最大需要量的城市输出货物和服务。①
以上两个缺陷已经被另一些研究者设法克服,使最小需要量法日益趋于完善。
为了避免第一个缺陷,莫尔(C.L.Moore)把城市按规模分成连续的14个等级,从每一个规模级的城市样本中,找出每个部门的最小职工比重和中位城市的规模。然后将两者进行回归分析,利用回归方程可以求到任何规模城市某部门相应的最小需要量。①数学表达式如下:
Ei=ai+bilgP (1)
式中
Ei——i部门P规模城市的最小需要量;
ai,bi——为参数。ai,bi用下式求得:
Eij=ai+bilgPi (2)
式中
Eij——第j规模级城市中第i部门实际找到的最小职工比重;
Pj——第j规模级城市的人口中位数。
表31 莫尔回归分析的相关指数(R2)
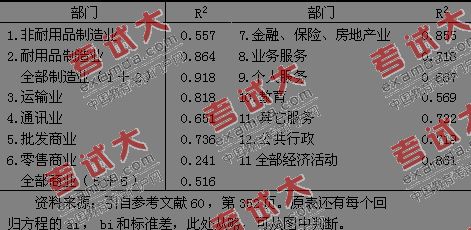
莫尔对1970年美国333个城市的分析结果表明(表31,图34),大多数部门的城市规模级与最小需要量之间有很高的正相关。出乎意料的是零售商业相关性不强。建筑业、健康服务业和农业则没有相关性,故没有包括在图表中。所有部门都表现出最小需要量随城市人口增加而上升的趋势,其中以耐用品制造业最显著。
为了克服乌尔曼等方法中的理论缺陷,吉布森(L.J Gibson)和沃登(M.A.Worden)改用各规模组中第2位最低的城市职工比重作为每个规模组城市的最小需要量。他们为了从各种方法中找出最佳区分基本/非基本的间接方法,曾经对亚利桑那州的20个小城镇(人口从1838人到15000人)用普查法、3种不同方式的抽样调查法、2种不同标准的区位商法和4种不同的最小需要量法进行对比研究。结果证明,用莫尔建立的最小需要量的回归模型所得的结果最接近于普查结果。用第2位最低职工比重的最低需要量法效果也相当好。①
(六)需要注意的问题
总之,为了避免用费时、费事又费钱的实际普查方法来取得城市的基本/非基本活动的结构,促使了许多种相对简单的间接方法的诞生。这些方法可以用一个表达式来概括:
Bi=Ai-αA
式中
Bi——某城市i部门的基本活动部分的职工;
Ai——某城市i部门的职工;
A——某城市的全部职工;
α——需要寻找的系数。
根据这个表达式可以看出,虽然上述各种方法的思想出发点各有差异,但在实际应用中,只是α的取值不同而已。在区位商法里,α取全国或区域的背景百分比值;在正常城市法里,取第五个百分位的城市的职工比重;在最小需要量法中,取所在规模组中职工比重最低的或次低的那个城市的数值,或建立回归模型取得。总的而言,区分基本/非基本活动的方法在不断完善。
尽管如此,在运用中仍有一些难题需要注意解决:
1.计量单位的选用
无论哪种方法,当区分基本/非基本部分时取用的指标不同,所得的结果是不同的。从经济基础理论的原意讲,以产品指标或收入指标比较理想,但常常物质生产部门与非物质生产部门之间无可比性。即使考虑城市产品或服务的输出收入,又常常排除了城市其它的基本收入来源,如外来的投资、政府的拨款、补贴等,这也是从城市以外得到的收入,而且对城市发展常常起重要作用。经常使用的劳动力指标,好处是资料易得,但它隐含的前提是同一部门的职工生产效率一样,人们的工资水平和消费结构一样,这一前提实际上并不存在。
2.地域单元的确定
基本/非基本活动的划分以供给外地或本地消费为标准。如果把地域缩小到每个企业单位,则它们的经济活动几乎全部是基本的;如果把范围扩大到全球,则几乎全部是非基本的。对城市也一样,使用不同空间尺度的城市地域界线,会取得不同的结果,相互间也无可比性。这一问题在国外大城市尤显突出。因为那些城市有大量通勤人员,常常在中心城市工作并取得收入,住在中心城市以外甚至中心县以外,并在居住地纳税和消费。按大都市区为地域单元时,这些人很大部分属于大都市区的非基本人口,但是按城市化地区等建成区概念计,他们却是所在居民点的基本人口。在我国应用时也会碰到类似问题。
3.部门单元的划分
部门单元划分粗一些或细一些,所得到的基本/非基本比例也不同。一般说来,部门分得越细,区位商法的结果就越准确。而最细的分类,却使各部门的最小需要量几乎都为零,结果城市就没有了内部需求,因此最小需要量法就适合于比较粗的部门分类。遗憾的是上述方法的所有作者,对于他们为什么分成36个部门或14个部门等都没有加以解释。至于象一个钢铁联合企业,假如最终输出产品是钢材,但本身有铁矿、烧结、炼铁、炼钢等生产过程,还有一套为自己和向社会开放的服务设施,类似这样的企业是归到一个部门还是分成若干部门计算基本/非基本活动,也没有理想的规定。
上述问题的提出,并非贬低研究城市基本/非基本构成的巨大意义。而是说明城市研究对象的特殊性,要求绝对的严密和准确是极为困难的。在城市地理学里,所谓可比性都是相对的。上述任何一种方法,包括普查的方法,所得的结果只是近似于实际而并不等于实际。城市地理学运用这一概念,也并不主要为揭示某一城市的基本/非基本活动的实际数量,主要目的是对比不同时间和不同空间里城市B/N比的差异规律和变化趋势。如果研究者根据各自研究的目的和可能得到的资料,注意使用同样的指标、同样的城市概念、同样的部门划分,吸取前人方法的优点,是能达到上述目的的。






