大型通用有限元软件ABAQUS由于具有强大的非线性求解器,在高层建筑大垮结构以及大型桥梁抗震分析中应用日趋广泛。在钢筋混凝土非线性分析中,要想获得较为理想的模拟结果,混凝土本构模型的定义最为关键。本文在前人的基础上,概述了ABAQUS混凝土本构模型的一些关键点,并对各个本构模型的使用范围作了简单的总结。
ABAQUS中提供了3种混凝土本构模型:脆性开裂模型(Brittlecracking),弥散开裂模型(Smeared crack)以及塑性损伤模型(Plasticitydamage)。三种本构模型具有不同的使用范围。
脆性开裂模型仅考虑混凝土的受拉非线性行为,适用于素混凝土或少筋混凝土结构构件中混凝土材料本构关系的模拟,主要用于水工大坝等结构的模拟。而对于正常配筋的混凝土结构,一般使用较多的为弥散开裂模型和塑性损伤模型,本文着重对这两个本构模型做一定的比较。
比较之前,首先说说ABAQUS中混凝土材料本构模型定义的一些要点。
混凝土弥散开裂模型和塑性损伤模型都需要定义混凝土材料的单轴受压应力-应变关系。根据混规,混凝土材料的单轴受压应力-应变关系由弹性段、强化段和软化段3 部分组成,如下所示:
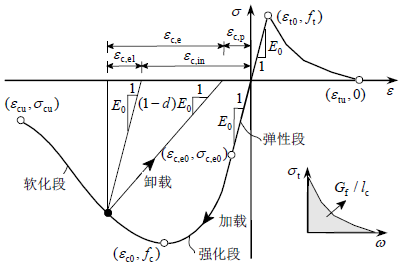
定义弹性段时,一般选择三分之一极限强度确定混凝土初始切线弹性模量,也即是:![]()
当混凝土受压应变超过弹性极限应变![]() 后,混凝土将进入强化段和软化段。混凝土材料单轴应力应变关系的强化段和软化段曲线为混凝土压应力
后,混凝土将进入强化段和软化段。混凝土材料单轴应力应变关系的强化段和软化段曲线为混凝土压应力![]() 与非弹性应变
与非弹性应变![]() 的关系,非弹性应变
的关系,非弹性应变![]() 的计算公式为:
的计算公式为:![]() ,另外,需要保证混凝土应力卸载至零时塑性应变
,另外,需要保证混凝土应力卸载至零时塑性应变![]() 大于零,其计算公式为:
大于零,其计算公式为:![]() 上式中,d 也即为混凝土在往复荷载作用下的损伤因子。
上式中,d 也即为混凝土在往复荷载作用下的损伤因子。
混凝土受拉骨架线中峰值应变前的应力-应变关系假设为线弹性,弹性模量和受压初始切线模量E0 相同,峰值应力ft 取![]() 。当混凝土拉应变超过受拉弹性极限应变
。当混凝土拉应变超过受拉弹性极限应变![]() 后将进入受拉软化段,混凝土受拉软化段曲线由混凝土拉应力
后将进入受拉软化段,混凝土受拉软化段曲线由混凝土拉应力![]() 与开裂应变
与开裂应变![]() 的关系确定。开裂应变
的关系确定。开裂应变![]() 的计算公式为:
的计算公式为:![]()
混凝土在应变超过受拉峰值应变后将产生开裂现象,裂缝模型是混凝土材料受拉本构模型的关键。混凝土受拉软化阶段的应力-应变关系一般采用直线形式,软化模量与混凝土断裂能以及混凝土单元特征尺寸有关。
ABAQUS 中提供了3 种定义混凝土单轴受拉应力-应变关系的接口,包括应力-开裂应变关系,应力-裂缝宽度关系,直接输入受拉断裂能。位置如下图:
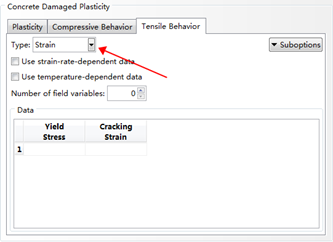
很多同学在定义单轴应力-应变关系时,习惯性采用应力—开裂应变模型,然而当有限元模型中混凝土单元的网格大小不一致时,应力-开裂应变关系也不同,这将增加建模的工作量,因此建议采用定义应力-裂缝宽度关系或直接输入断裂能的方法来定义混凝土单轴受拉行为。
下面将具体说说弥散开裂模型和塑性损伤模型的一些区别。
所谓弥散开裂模型,也即是将实际的混凝土裂缝弥散到整个混凝土单元中,将混凝土材料处理为各向异性材料,利用混凝土的本构关系来模拟裂缝的影响。通过剪切模量折减系数可以有效的避免剪力锁死现象。
该模型屈服准则与经典弹塑性理论中的Drucker-Prager准则一致,流动准则则为普通的关联流动法则,同时该准则无法考虑混凝土在往复荷载作用下的卸载刚度退化和再加载刚度恢复等往复受力特征。因此该准则适用于模拟以剪切行为为主的结构构件,如深梁、钢筋混凝土或钢管混凝土节点核心区等,不适用于往复荷载作用下的构件模拟。
常用软件ANSYS混凝土本构模型定义也是基于弥散开裂模型,这也是为什么在ANSYS中无法考虑结构材料损伤,单就其混凝土非线性模拟结果这块,其效果不如ABAQUS.
塑性损伤模型假定混凝土的破坏形式是拉裂和压碎,混凝土进入塑性后的损伤分为受拉和受压损伤,分别用2 个独立的损伤因子来模拟由损伤引起的弹性刚度退化。引入损伤指标,通过对混凝土的受拉和受压弹性刚度加以折减,来模拟混凝土的卸载刚度随损伤的增大而降低的特性。
这里重点介绍两个参数:损伤因子d以及刚度恢复系数。
所谓损伤因子,是指混凝土弹性卸载时的弹性模量相对于初始切线弹性模量的折减。计算公式为:
E= (1- d)E0
式中:E 为混凝土弹性卸载时的模量;E0 为混凝土初始切线弹性模量;d =0 表示无损伤,即混凝土的卸载模量与初始切线弹性模量完全相同,d =1 表示完全损伤,即混凝土的卸载模量为零。过程图如下:
从压到拉滞回准则:
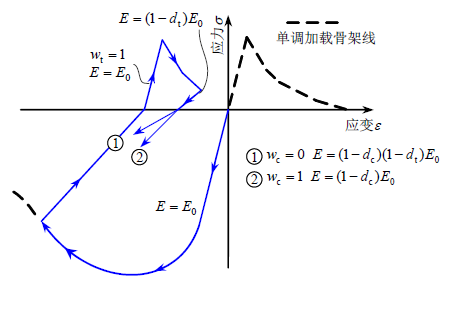
从拉到压滞回准则:
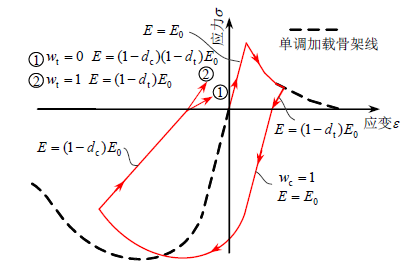
上面图中,w表示刚度恢复系数,分为受拉刚度恢复系数Wt以及受压刚度恢复系数Wc。分别表示混凝土应力-应变曲线从受拉区过渡到受压区和从受压区过渡到受拉区时,弹性模量的变化程度。
Wc=1表示混凝土从受拉区进入受压区时弹性模量可完全恢复至上一次受压卸载时的弹性模量,Wc=0表示混凝土弹性模量不能恢复。Wt=1表示混凝土从受压区进入受拉区时弹性模量可完全恢复至上一次受压卸载时的弹性模量,Wt=0表示混凝土弹性模量不能恢复。
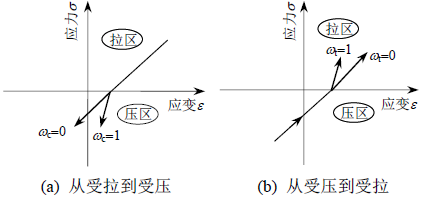
ABAQUS默认Wc=1,Wt=0,实际分析时,按默认值取即可。
ABAQUS的损伤因子与恢复系数的定义位置如下:
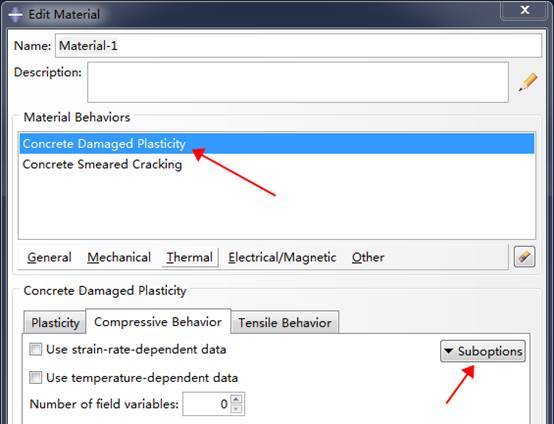
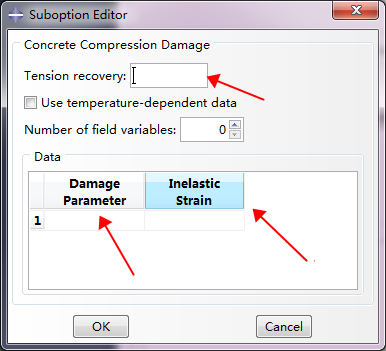
混凝土损伤因子与混凝土的非线性程度有关,因此如果想要获得比较良好的混凝土非线性模拟结果,找到一个合适的损伤模型是比较关键的,常用的计算公式如下:
受压损伤因子:
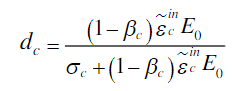
受拉损伤因子:
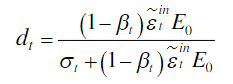
关于混凝土定义的其他一些参数取值参考值如下:
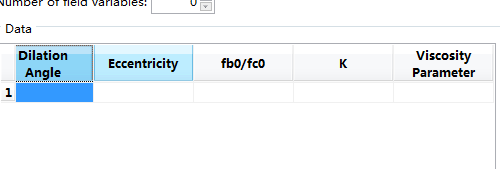
Dilation Angle: 37-42
Eccentricity:0.1
Fb0/fc0:1.16
Kc:0.667
Visosity Parameter: 0.0005