PKPM与Midas Building结构计算结果的比较
[摘要] 本文分别用PKPM与Midas Building对5个平面和立面均规则的建筑进行了结构计算。比较了计算出来的质量,周期,风力,地震力,最大层间位移角及其结果差异的大小,最后分析了计算结果差异产生的原因。
[关键词] PKPM;Midas Building;结构设计;计算误差
1. 引言
PKPM是国内建筑设计行业使用最普遍的软件,Midas Building也算是国内主流的建筑结构设计软件中比较有名的一个,由于其界面友好,使用方便,受到了越来越多的中国建筑设计人员的认可。有建筑结构设计者发现,用这两种结构计算软件会得出不一样的结果。但是到底这种结果的不一致性多大以内是可以接受的范围还没有定论。不少人就以工程精度10%以内即可认为两者是相等的概念为准。事实上,产生这种误差的原因有三个方面,数值计算精度差异,参数的差异和人工输入误差。数值计算精度的差异非常的小,通常不会超过百万分之一。软件内部参数设置的差异和人工输入误差通常是造成明显计算结果差异的原因。使用某软件做设计之前充分了解的该软件内部参数设置所产生的特性是很有必要的。
本文主要比较两个软件计算出来的质量,周期,风力,地震力及最大层间位移角(不讨论如配筋这样的详细指标)。
2. 模型说明
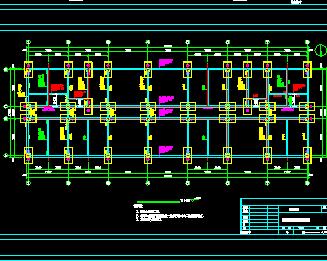
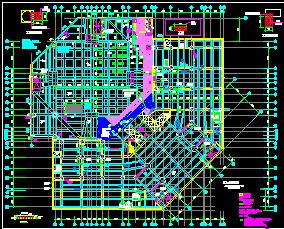
为了比较PKPM和Midas Building这两个结构计算软件,这里设计了5个平面简单,两轴对称(除了次梁分布以外)的建筑(图 1),其中4层,8层,16层这三个建筑为纯框架结构,30层,45层的这两个建筑为框架-核心筒结构。由于这5个建筑模型仅仅是用于对比PKPM和Midas Building的计算结果差异,所以为了简便,这5栋楼的宽度均设为28.8米。平面x,y轴方向均为4跨每跨7.2米的对称平面。而且首层层高跟其他层层高相同,均为4米。框架-核心筒结构的核心筒宽度为14.4米。为了简便,筒体上没有开洞,没有连梁。楼板厚度均设为120mm。加在楼板上的恒荷载(除了楼板自重)和活荷载的标准值分别设为3kN/m2和2kN/m2。这5个结构不考虑地下室,嵌固端在首层的柱脚位置。这5个建筑模型的具体参数在表 1总结。
这5个建筑都被假设建在广东深圳,设计地震分组为第一组,地震烈度7度(0.1g),场地类别设为二类。周期折减系数和计算的振型数如表 1所示。修正后基本风压为0.75kN/m2。地面粗糙度类别设为B类。计算风荷载时使用的周期是由特征值分析计算得出。荷载的加载方式为一次性加载,不考虑施工过程的影响。由于这5个建筑的刚重比均大于2.7,所以重力二阶效应没有考虑。
这5个建筑分别用PKPM和Midas Building建模。对比软件时需要保持模型的一致性,所以这两个软件建模时使用了以下的共同的参数设置:1. 完全相同的材料和构件尺寸;2. 不去除梁柱节点处重叠部分反复计算的质量;3. 每层均采用刚性板假定; 4. 相同的剪力墙和楼板平面单元的网格分割尺寸;5. 特征值分析时均采用子空间迭代法,取相同的振型数量;6. 相同的各种荷载设定参数。
3. 结构分析
图 2(a)(c) 分别表示的是两个软件计算出的各个建筑的总质量和第一振型的自振周期(每栋楼的第一振型均为y方向(图 1)的平动方向),而图 2 (b)(d)表示的是它们的差异。差异由式(RPKPM-RMidas)/ RMidas计算得出,其中RPKPM与RMidas分别代表PKPM和Midas Building计算的结果。图 2中的横轴表示的是楼的总层数。由图 2(a)(b)可以看出,PKPM和Midas Building的总质量的差异非常小,而且无论是哪栋建筑这个差异都是一致的(-1.94%)。这个恒定的差异是两个软件对重力加速度取值不同而造成的。PKPM和Midas对重力加速度的取值分别为10m/s2和9.806m/s2。而PKPM和Midas计算出来的质量比恰好就是0.9806。
由图 2 (c)可见,两个软件计算出的30层和45层的框筒结构的周期差异比较小,结果几乎是重叠的,其差异小于1%(图 2 (d)),而4,8和16层这三个框架结构的差异相对较大,最大达到8.2%(图 2 (d))。
图 3左列和右列分别表示的是两个软件计算出的作用在结构上(图 1的y方向)的风力和地震力。根据左列的5张图可以发现,风力总体比较接近,尤其是在楼层上部。在16,30和45层建筑的中下部,由于PKPM跟Midas用的计算顺风向风振系数βz的结构第1阶振型系数Φ1(z)(文献[1] )不一样,PKPM的风力略微高于Midas的,层风力最多高18.8%。而4层和8层的结构由于不用考虑顺风向风振,其所受风力完全相等。
根据右列的5张图可以发现,两个软件计算出的30层和45层的框筒结构的地震力比较接近,而4,8和16层的框架结构建筑的地震力差异相对比较明显。
图 4表示的是由风力和地震力引起的最大层间位移角(图 1的y方向)。总体来看,PKPM计算出的结果高于Midas。相比框筒结构,其差异在框架结构表现得比较明显。其中16层的框架结构在风荷载和地震荷载引起的最大层间位移角的差别分别为28.6%和16.4%。
4. 补充分析
理论上,两个软件用同一个计算方法会得出极其接近的结果(仅有数值计算的误差),比如地震力和由地震引起的层间位移角。因为地震力的分布是由质量分布和刚度分布决定的(使用经典阻尼的情况下)。如果这两个要素完全相等的话,地震力分布应该是完全相等的。然而从上面的分析(图 3,图 4)来看这两个软件计算结果的差别虽然大致上是工程上可以接受的精度范围之内,却没有达到数值分析的精度。然而是什么造成这种误差呢?从图 2 (a)(b)可知两个软件分别计算出来的总质量的差异很小,而且是恒定的。如果其节点质量分布也是一致的话,造成这种明显结果差异的原因应该在刚度分布上。结构设计软件对常规建筑的结构设计的过程是:建立模型,调整模型,计算内力,调整内力,计算变形和配筋。调整模型和调整内力这两个阶段通常是不同软件产生不同计算结果的原因。在形成总刚度矩阵之前,梁的刚度是经过调整的。国家规范(文献[2] )称:“在结构内力与位移计算中,现浇楼盖和装配整体式楼盖中,梁的刚度可考虑翼缘的作用予以增大。近似考虑时,楼面梁刚度增大系数可根据翼缘情况取1.3~2.0”。由此可见这个增大系数比较主观,这两个软件对该增大系数的取值可能不同。所以接下来进行一组未对梁的刚度进行放大的5个建筑模型的分析,这些模型的其他参数设置与前面的分析模型完全相同。 图 5中的Case1和Case2分别表示的是梁刚度放大和梁刚度未放大的情况。其中图 5(a)(b)中的Case1与图 2 (c)(d) 是完全相同的。由图 5(a)可以看出,跟梁刚度未放大的情况相比,梁刚度放大的情况下抗侧向力刚度增加,周期变短。这种现象在框架结构的4,8和16层建筑上表现得尤为明显,而框筒结构的30层和45层建筑的周期相对变化较小。
由图 5 (b)可见,梁刚度未放大时由两个软件计算出的周期的差异均小于1.1%,而且差异是恒定的。梁刚度放大时框筒结构的差异比较小(小于1%),但纯框架结构的差异最大达到8.2%。这个是因为虽然梁刚度放大之后会增加纯框架结构的抗侧向力刚度,但框筒结构的中的筒体的抗侧向力刚度远远大于框架部分,所以梁的刚度放大对整个框筒结构的贡献是比较小的。所以两个软件使用不同的梁刚度放大系数时纯框架结构的结果差异比较大但框筒结构的结果差异比较小。
图 6表示的是两个软件分别计算出的作用在结构上(图 1的y方向)的风力和地震力。对比图 6和图 3左列的5张图可以发现,它与考虑梁的刚度放大系数时的情况是很接近的。因为考虑梁的刚度放大时周期的变化并不是特别大(图 5),因而计算出来的顺风向风振系数的差异较小。
从图 6右列的5张图可以发现,两个软件计算出的地震力非常接近,结果几乎是重叠的。跟图 3右列的5张图比较可知,图 3中造成地震力分布不一致原因就是梁的刚度放大系数。
图 7表示的是由风力和地震力引起的最大层间位移角(图 1的y方向)。横轴的最大值是1/550。总体来看最大层间位移角吻合得比较好。最大差别为6.5%。
根据图 7左列的5张图可以发现,4层和8层的建筑由风力引起的最大层间位移角几乎完全相等,16,30和45层的建筑由于在PKPM里所受风力略大(根据图 6,层风力最大差18.5%),其由风力引起的最大层间位移角也偏大一些(最大6.5%)。
根据图 7右列的5张图可以发现,由地震引起的最大层间位移角非常的接近,结果几乎是重叠的。跟图 4右列的5张图比较可进一步确定造成图 4中地震力分布不一致原因就是梁的刚度放大系数。
最后,这两个软件计算出的结果差异在图 8中总结。其中图 8的纵轴表示的是5个建筑模型当中得出的最大差异。总体来看,无论梁刚度是否放大,总质量的差异都是不变且恒定为1.94%的。风力的差异也比较恒定,均略微超过18%。
不考虑梁的刚度放大系数时周期,地震力及其引起的最大层间位移角的差异非常小,均小于1.1%。
考虑梁的刚度放大系数时周期和地震力的差异分别为8.2%和5.7%,还算符合工程精度。然而,风力及地震力引起的最大层间位移角的差异较大,分别为28.6%和16.4%。最大层间位移角作为判断侧向刚度是否足够的大指标,这种差别是不能忽略不计的。
5. 结论
本文通过对5个平面和立面均规则的建筑模型的结构分析对比了PKPM和Midas Building的计算结果,并得出了以下结论:
1. 用PKPM与Midas Building进行结构计算得出的由风力和地震引起的最大层间位移角差别较大,最大值分别为28.6%和16.4%;
2. 在不考虑梁刚度放大的情况下PKPM和Midas Building计算出的周期,地震力及其引起的最大层间位移角非常的接近(差异小于1.1%),可以作为检验用两个软件建立的模型是否完全一致的标准;
3. 在不考虑顺风向风振的情况下,PKPM和Midas Building计算出来的风力是完全相等的。在考虑风振的情况下,层风力的最大差异达到18.5%。
参考文献
[1] 建筑结构荷载规范GB50009-2012,中国建筑工业出版社,北京,2012
[2] 高层建筑混凝土结构技术规程JGJ3-2010,中国建筑工业出版社,北京,2010