摘要:桩基础是一种常用的深基础形式,它由桩和桩顶的承台组成。按桩的受力情况,桩分为摩擦桩和端承桩两类。桩的沉降分为单桩和群桩两种沉降。单桩受到荷载后,其沉降量由下述两部分组成:桩自身的压缩变形和桩底以下土层的压缩。目前,计算单桩沉降量的计算方法主要有分层总合法、弹性理论法、荷载传递分析法、剪切变形传递法、有限元法及其他简化算法,这些方法都是在一定的简化基础上考虑一种或几种因素对桩基沉降量的影响。而对于群桩的沉降计算;当桩都为端承桩时,由于不需要考虑群桩效应,故可将单桩的沉降作为整个桩基础的沉降;当桩都为摩擦桩时,由于要考虑桩与桩之间的相互影响、承台的影响等。其沉降计算方法有整体分析法、等代墩基法经验法。
关键词:桩基础 计算方法 沉降
桩基础的承载力与沉降是桩基设计中的重要内容,沉降常常是设计中需控制的一个重要因素,与承载力相比,沉降的计算更为复杂。在过去漫长的时间内,从事岩土工程的研究者和工程师们,为了精确计算和预测桩基的沉降,曾进行过大量的研究,提出过一系列的计算桩基沉降的方法,但由于地下桩基础的复杂性和地基土的非均匀性,桩基础沉降的计算理论还有待成熟。
1.单桩沉降计算方法
单桩的沉降与桩的长度、桩周及桩底土的性质、荷载大小及持续时间等因素有关。计算单桩单桩的沉降则应采用长期施加的荷载。
1.1剪切变形传递法
Cooke(1974)提出了摩擦桩荷载传递的物理模型,该模型为了简化计算,作了一系列假定并认为:当荷载较小时,桩的沉降较小,桩土之间不产生相对位移,上下土层之间无相互作用, 桩的沉降由剪切变形的积累而产生的,剪应力从桩侧表面沿径向向四周扩散到周围土体中;摩擦桩一般在工作荷载作用时,桩端承担的荷载比例较小,沉降主要是由桩侧传递的荷载所引起,在单桩周围形成漏斗状位移分布。
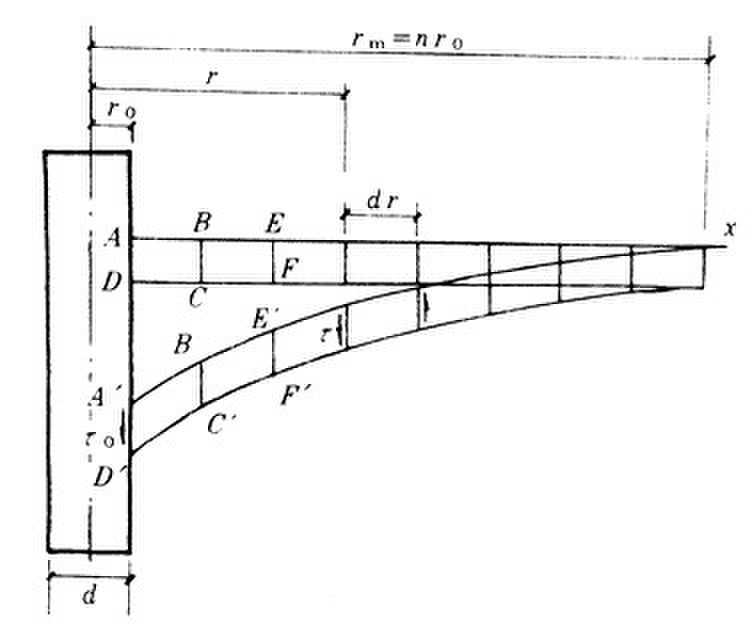
宰金铭(1993,1996)将剪切变形传递法推广到塑性阶段,从而得到桩周土非线性位移场解析表达式。在该基础上,与层状介质的有限层法和结构的有限元法联合应用,给出群桩与土和承台非线性共同作用分析的半解析半数值方法。
1.2荷载传递分析法
荷载传递分析法亦称传递函数法,由Seed及Reese于1957年提出,它是目前应用最为广泛的简化方法,这种方法是从规定的荷载变形传递方式来计算桩对荷载的反应。其基本思想是:将桩划分为一系列等长的桩段(弹性单元),每一桩段与土体之间的联系用非线性弹簧来联系,桩端处土体也用非线性弹簧与桩端联系,以模拟桩-土之间的荷载传递关系。
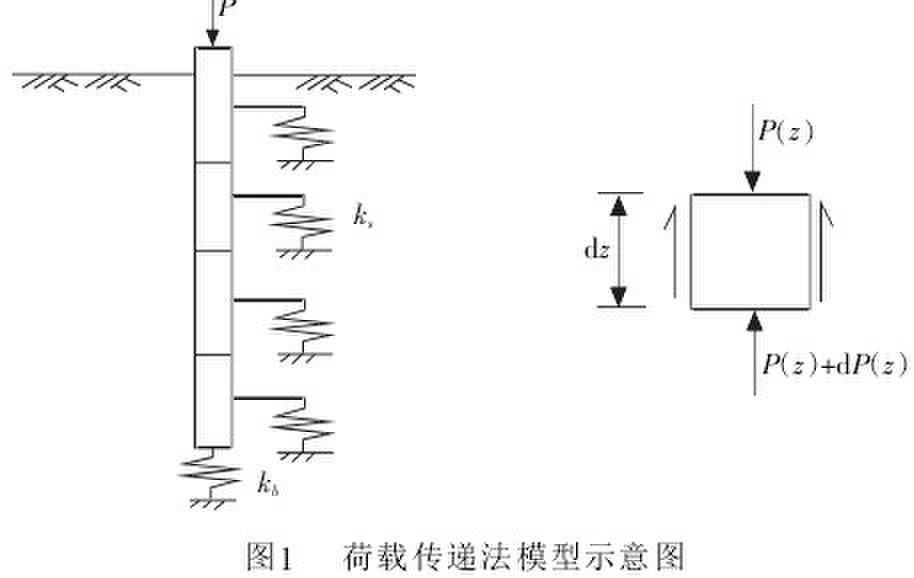
Guo(2001)提出了一种弹脆塑性模型,以考虑桩周土体的软化性状,这也是三折线模型中的一种。
将桩与土之间的接触简化为弹簧连接,易推得
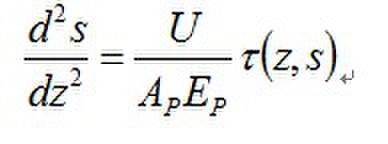
式中的 即桩侧阻力的传递函数,只要该函数能够确定,解上述方程即可得到桩的位移。
1.3弹性理论法
弹性理论法于20世纪60年代被提出,它将土体视为弹性半无限体,依靠Mindlin解,建立桩、土之间的变形协调方程,最终求得桩的轴力、侧阻、端阻及沉降等。。以弹性理论法为根据发展出一些计算单桩沉降的方法,这些解法虽略有不同,但一般都基于桩的位移与临近土位移的协调条件,为此,借助于轴向荷载下桩身的压缩求得桩的位移,又应用荷载作用于半无限体内某一点所产生的Mindlin位移解求得桩周土体的位移。由于弹性理论假定桩土界面普遍满足弹性即界面不发生滑移这一条件,沿界面诸相邻点的桩位移应与土位移相等,桩侧完全粗糙,桩侧阻力沿每个单元周围的分布是均匀的;忽略桩、土之间在法向的变形协调。由此依靠即可求得桩身摩阻力和桩端阻力的分布,并进而求得桩的位移分布。吕凡任(2004)提出了考虑桩土相对位移的“广义弹性理论法”从而可以考虑桩周土的塑性,并将其应用于斜桩分析。
2.群桩沉降计算方法
桩基础的应用大都是以群桩的形式出现,群桩效应在群桩沉降问题中表现的非常明显。端承桩通常不需要考虑群桩效应,故可将单桩的沉降作为整个桩基础的沉降,但对于摩擦桩来说,计算桩基沉降时,应考虑桩与桩之间的相互影响、承台的影响等因素。
2.1整体分析法
整体分析法,目前应用较广泛和成熟的整体分析方法主要包括有限元法、边界元法和弹性理论法。有限单元法是适应计算机应用而发展起来的一比较新颖和有效地数值计算方法,随着计算机的发展,有限元越来越广泛。常用的桩基有限元分析软件有ABAQUS ,ANSYS ,MARC,和ADINA等其它的还有Plaxis和FLAC/FLAC3D等等。研究表明,有限单元法的计算结果与现场观测结果非常相似。由于受计算参数较多,三维计算要求内存大,计算时间长,其使用范围受到影响。不过,作为探索和校核实用简化方法的工具,有限单元法仍有着重要的实际意义。从长远地来看,它仍然是计算群桩沉降的一种趋势和正确方向。由于桩土作用的复杂性和单桩沉降理论仍在进一步完善中,为了方便和辅助桩基设计,产生了一些简化方法,如神经网络法,大直径桩、嵌岩桩沉降计算法等。这些方法现在尚处于讨论验证阶段,其精确性受到较大限制。因此,这些方法存在较大局限性。
边界元法也叫积分方程法,是把区域问题转化为边界问题求解的一种方法,即将筏板地基中的桩进行离散化分析。单纯的边界元法假设桩土界面位移协调,没有考虑桩土界面土的屈服滑移,与实际工程有一定差距。Sinha (1996)提出了一种完整的边界元法,把桩离散用边界元法分析,用薄板有限元法分析筏板,土被假定为均质弹性体,引入了土的滑移现象,以分析土体的膨胀或固结效应。有限条分法首先用于分析上部结构,并取得成功。Cheung(1976)首先提出将有限条分法用于单桩分析,以分析层状地基中的单桩的特性。
用弹性理论法算群桩的沉降与计算单桩沉降的方法完全相似,其土的位移方程可写为

采用弹性理论法和有限元法分析群桩时,发现群桩将大部分荷载传到了地基的深部,水平方向扩散的应力很小,桩端附加应力受桩数、桩长径比、桩的距径比和吃力层刚度的影响较大,而受承台长度比和桩土相对刚度比影响较小。
2.2等代墩基法 (实体深基础法)
等代墩基法是现在工程界应用最广泛的一种计算群桩沉降的方法,该计算模式是将承台下的桩基础及桩间土看作一个实体基础,并忽略其变形;在此等代墩基范围内,桩间土不产生压缩如同实体墩基一样工作,然后按照浅基础的沉降计算方法来计算群桩的沉降。等代墩基法适用于桩距不大于6倍桩径的群桩。该方法计算简单,但由于高估了墩基底面的压力,导致了压缩层深度增加。由于计算时考虑的前提条件不同,研究者提出和使用着计算的不同模式,其主要差别在于选用的假想实体基础底面的位置不同,以及对地基土中附加应力的考虑和计算不同根据桩距地基土的性质不同,桩间土实际上是会产生不同程度的压缩变形,另一方面假想的实体基础外围存在着侧面剪应力的扩散作用,为了消除这些差别对群桩沉降计算的影响,人们采取了一些措施,集中表现在所采用的模式上。这些措施是:
1.变动假想实体基础底面的位置,以考虑桩间土存在压缩变形的可能,这是Peck和Terzaghi等人建议的模式Peck等建议将假想实体基础底面置于桩端平面以上 高度处, 取为桩长的1/3处(桩位于均匀并土中时)或进入持力层深度的1/3(桩穿过软弱土层并进入坚硬土层时〕这种建议涉及的影响因素过于单一,因为假想基底位置上升的因素很多,采用此法不能全面反映这些情况。
2.考虑墩基侧向摩阻力的扩散作用,从群桩桩顶外围按扩散角 向下扩散增大假想实体基础底面积,以考虑桩群外围总剪应力对沉降分析的影响,这是Tomlinson等人的模式。
3.为了改善地基土附加应力估计的精度,近年来国内外根据半无限弹性体内集中力的Mindlin公式发展了一些估计桩基荷载作用下地基土附加应力的方法,还有一种将Mindlin解与Boussinesq解对比来估计等代墩基的等效基底附加应力。
由于群桩沉降涉及的因素很多,至今还没有一种既能反映土的非线性、、固结和流变性质,又能在漫长的沉降过程中反映出桩与土的界面上相互作用力不断变化性状的计算模式。
3.计算方法评述
剪切变形法对深长桩的沉降计算较准确。但由于该方法忽略了竖向应力、径向位移对剪应力的影响、土参数随深度的变化及桩端沉降因素等诸多因素,会得到不合理的沉降,因而在桩基设计的实践中应用较少。
荷载传递法较弹性理论法,其计算要简单些。由于工程中的土大多数是分层的,应力土体的参数都随深度变化,因此荷载传递法沿深度将桩身分段的方法能准确反映桩承载特性。但是缺点是任意点桩的位移只与该点的摩阻力有关,忽略了其它方向的力及其它点的影响,没有考虑土体连续性,不能用于群桩的计算。
弹性理论法已经比较成熟,考虑土的连续性,可用于群桩分析,计算结果较准确。但其缺陷在于把地基看作均匀的、各向同性的理想弹性体,桩土之间无切向相对位移,忽略了实际中存在的应力及时间效应,需要进一步改进和完善。
整体分析法优点在于:有限单元可方便地反映岩土材料的复杂结构关系;有限元法对复杂的边界条件的反映比其他数值方法有较大的优势;开发了不同类型的单元,可以适合不同情况的模拟(如板壳单元模拟板壳的作用、界面单元模拟各种界面的特性);可以考虑各种复杂因素对桩基础沉降的影响。不足之处是实际计算中要考虑桩对土的影响范围,需要对土体划分大量的单元。此外,为了保证精度,必须将单元划小,使得单元数目急剧增加。这些都增加了计算时间。边界元法能够较准确计算群桩的沉降,边界元法可方便地反映岩土材料的复杂结构关系,单纯的边界元法假设桩土界面位移协调,没有考虑桩土界面土的屈服滑移,与实际工程有一定差距。
等代墩基法是一个科学、实用的计算方法,能反映群桩基础的各因素对沉降的影响,如桩的距径比、长径比、桩数等。其存在的问题是对于长桩,特别是桩侧土较好的长桩基础,计算沉降量与实测值误差较大,统计结果发现,实测值往往比计算值小很多。造成这种现象的原因是高估墩基地面的应力,这样造成了压缩层深度的增加,虽然用沉降修正系数或等效作用系数进行修正,但是计算值仍保守,较实测值大。
4.结语
本文对目前国内外桩基础的沉降计算理论进行了分析,包括单桩和群桩的沉降分析,并对它们的优缺点和适用范围进行了论述,在实际应用中,应用何种方法要视当时的地质条件等因素而定。
参考文献:
[1] 赖琼华. 桩的P-S曲线计算方法[J]. 岩石力学与工程学报,2003,22(3):509~513
[2]. 滕延京,宫剑飞. 李建民基础工程技术发展综述[J].土木工程学报.2012(05).
[3].毛泽华摘译自《Geotechnique),1999(4)国外公路,2000Vol.20No.4.
[4].《桩基工程手册》编写委员会.桩基工程手册.北京.中国建筑工业出版社,1995.
[5].何颐华,王铁宏.大直径扩底桩承载力及沉降变形的计算.建筑结构学报.Vol. 14.No.2 1993.4
[6]黄强.桩基工程若干热点技术问题[M].北京:中国建材工业出版社,1996.
[7]陈龙珠,梁国钱,朱金颖.桩轴向荷载--沉降曲线的一种解析方法[J].岩土工程学报,1994(16)
[8] ( GB50007 - 2002)建筑地基基础设计规范[S].北京:中国建筑工业出版社,2005.
[9]韦登,徐远前,陈福江.浅析群桩沉降计算方法,四川建筑,2008(11)
[10]李朝晖.关于桩基沉降研究现状,工程建筑,2009(6)
[11]王宏凯.试论建筑桩基在施工中沉降问题及解决办法,赤子,2009(8)
[12].宰金IN,宰金璋.《高层建筑基础分析与设计》.北京:中国建筑工业出版社,1993.
[13] 赖琼华. 桩的沉降计算在工程中的应用,广东水利水电,2002
[14] 陈国兴. 高层建筑基础设计[M]. 北京:中国建筑工业出版社,2000
[15] 复习教程编写组. 注册岩土工程师专业考试复习教程[M]. 北京:中国建筑工业出版社,2002
[16] 赖琼华. 岩土变形模量取值研究[J]. 岩石力学与工程学报,2001(增)
[17] 李素华,吴世明,刘忠孝. 工程桩质量检测技术中的若干问题探讨[J]. 岩石力学与工程学报,2002,21(1)
[18] 蒋企,古晋雄,戴永相等. 桩基施工质量监督的新途径[J]. 岩石力学与工程学报,1998,17(3):341~344
[19] 徐礼华,刘祖德,茜平一. 上部结构-桩基础-地基相互作用体系地震反应分析[J]. 岩石力学与工程学报,2002,21(11)
[20] 陆培炎,徐振华. 地基的强度及变形计算[M]. 西宁:青海人民出版社,1978
[21] 吴永红,郑刚,闰澎旺.多支盘钻孔灌注桩基础沉降计算理论与方法,岩土工程学报,2000,22(5):528-531.