网络计划工期优化在工程进度管理中的应用
摘要:简要介绍网络计划技术, 分析了资源有限, 工期最短及工期—成本优化原理, 并通过实例表示优化计算的方法与过程。并以银山型钢铁水预处理工程为例,通过网络计划优化技术找出工程关键线路,对优选系数最小的关键工作进行压缩和调整,使延期节点后续工作的工期由130d 缩短到115d,满足了施工工期要求。
关键词:网络计划;工程进度;工期优化;工期最短;关键线路
网络计划技术是工程项目计划管理的有效方法, 也是管理系统工程中的一项重要的现代管理技术。与传统的横道计划相比, 网络计划有其独到的优点: 能将施工过程中的各有关工作组成一个有机的整体, 全面而明确地表达出各项工作开展的先后顺序及相互制约和相互依赖的关系; 能准确进行各种时间参数的计算; 能在计划中找出决定工程进度的关键工作, 便于计划管理者集中力量抓主要矛盾, 确保工期; 在计划执行过程中, 可以预见某一工作由于某种原因推迟或者提前完成对整个计划的影响程度, 并根据变化的情况迅速进行调整; 利用网络计划中反映出的各项工作的时间储备, 更好地调配人力、物力,以达到降低成本的目的; 使计算机在建筑施工计划管理中得以应用。
以莱钢银山型钢铁水预处理工程为例,此工程是为进一步优化铁水品质而新建的工程,设计年处理铁水能力约530万t。施工内容主要包括厂房和设备钢结构平台的制作安装,以及扒渣、搅拌设备的安装施工。计划开工日期2010年1月17日,工期总日历天数为190d。原计划是在行车设备安装验收完成后,利用行车进行厂房内部钢结构平台及设备吊装,但是由于行车设备延期到货,致使其安装验收推迟了15d,并且该工作处于网络计划的关键路线上,影响了后续工程的施工,从而将导致总施工工期的延迟。为保证工程按时交工,对工程工期进行优化。
网络计划工期优化的原理及方法
工期优化原理:网络计划的优化是指在一定的约束条件下,按既定目标对网络计划进行不断改进,以寻求满意方案的过程。网络计划的优化目标应按计划任务的需要和条件选定,包括工期目标、费用目标和资源目标。根据优化目标的不同,网络计划的优化可分为工期优化、费用优化和资源优化3种。由于本工程网络计划的计算工期不能满足要求工期,所以需进行工期优化。
工期优化方法:网络计划工期优化的基本方法是在不改变网络计划中各项工作之间逻辑关系的前提下,通过压缩关键工作的持续时间来实现工期目标要求。按照经济合理的原则,在工期优化过程中,应选择优选系数或组合优选系数最小的工作进行压缩,不能将关键工作压缩成非关键工作,也不能将关键线路压缩成非关键线路。此外,当工期优化过程中出现多条关键线路时,必须将各条关键线路的总持续时间压缩相同数值;否则,不能有效地缩短工期。
工期优化步骤:1)确定初始网络计划的计算工期和关键线路。2)确定初始网络计划的关键线路,并计算应缩短的时间。3)选择应进行压缩的关键工作。选择压缩对象时应首先选择那些缩短时间后对质量和安全影响不大、有充足备用资源且缩短持续时间时所需增加的费用最少的工作。4)将所选定的关键工作的持续时间压缩至最短,并重新确定计算工期和关键线路。不能将关键线路压缩成非关键线路或将关键工作压缩成非关键工作。若被压缩的关键工作或关键线路发生改变时,则应延长其持续时间,使之仍为关键工作和关键线路。5)当计算工期仍超过要求工期时,则重复上述2)~4),直至计算工期满足要求工期或计算工期已不能再缩短为止。6)当所有关键工作已达到能缩短的极限而寻求不到继续缩短工期的方案,但网络计划的计算工期仍不能满足要求工期时,应对网络计划的原技术方案重新审定和调整。
网络工期优化实施
银山型钢铁水预处理工程原双代号时标网络计划如图1 所示。由网络计划图可知,要保证工程按期进行试车验收,必须保证⒆节完成,由于行车设备延期投用将影响其后续工作⑿→⒁→⒄→⒆、⑿→⒁→⒂→⒄→⒆、⑿→⒁→⒂→⒅→⒆和⑿→⒂→⒄→⒆的顺利开展,导致总工期拖延,所以该网络计划已经不能满足工期目标要求,必须对其进行调整优化。需要调整的各项工作的持续时间及优选系数如表1 所示。
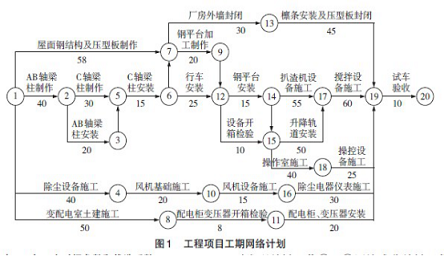
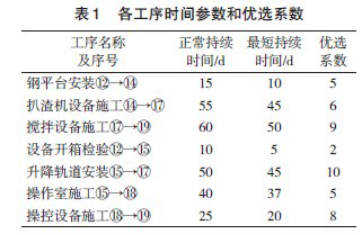
表1 中各个工作的优选系数是综合考虑质量、安全和费用增加情况而确定的。在选择关键工作压缩其持续时间时,应选择优选系数最小的关键工作。若需要同时压缩多个关键工作的持续时间时,则它们的优选系数之和或是组合优选系数最小的工作作为压缩对象。由于行车设备延期到货15d,故需要对其工期压缩15d。具体过程如下:
第一次压缩。1)根据各项工作的正常持续时间,通过用标号法确定网络计划的计算工期为130d,关键线路为⑿→⒁→⒄→⒆。2)计算应缩短的时间:△T=Tc (网络计划的计算工期)-Tr (要求工期)=130d-115d=15d。3)由于此时关键工作为⑿→⒁,⒁→⒄和⒄→⒆,而其中⑿→⒁的优选系选数最小,故应将⑿→⒁作为优先压缩对象。4)将关键工作⑿→⒁的持续时间压缩至最短持续时间10d。第一次压缩后的计算工期为Tc=10d+55d+60d=125d,由于此时网络计算工期为125d,仍大于要求工期,所以需要继续进行压缩。
第二次压缩。1)用标号法确定网络计划的计算工期和关键线路仍为⑿→⒁→⒄→⒆。2)计算应缩短的时间:△T1=125d-115d=10d。3)由于此时关键工作为⑿→⒁,⒁→⒄和⒄→⒆,由于⑿→⒁时间已压缩至最短,其优选系数变的无穷大,已不能再进行压缩,在⒁→⒄和⒄→⒆中工作前者的的优选系数最小,故应将其作为优先压缩对象。4)将关键工作⒁→⒄的持续时间压缩至最短持续时间45d,重新确定关键线路和计算工期。此时发现关键工作⒁→⒄压缩成非关键工作,按照网络优化原则应将其持续时间延长为50d,使之成为关键工作。工作⑿→⒁恢复为关键工作之后,网络计划中出现2条关键线路,即:⑿→⒁→⒄→⒆和⑿→⒂→⒄→⒆。由于此时计算工期为Tc=10d+50d+60d=120d,仍大于要求工期,故需要继续压缩。
第三次压缩:需要缩短的时间△T2=120 d-115d=5 d。因为⑿→⒁的工作时间已压缩至最短,不能再继续进行压缩,所以有以下3 种方案:A 同时压缩工作⑿→⒂和工作⒁→⒄,优选系数为2+6=8;B 同时压缩工作⒁→⒄和工作⒂→⒄,优选系数为10+6=16;C 压缩工作⒄→⒆,优选系数为9。在上述压缩方案中,由于方案A 的组合优选系数最小,故应选择同时压缩工作⑿→⒂和工作⒁→⒄,将这2项工作的持续时间各压缩5d,再重新确定计算工期和关键线路。此时,关键线路有2条,⑿→⒁→⒄→⒆和⑿→⒂→⒄→⒆。计算工期为Tc=115d,等于要求工期,满足了工程施工的工期要求。
一项大型的工程是一个庞大的系统, 在工程施工过程中, 需要消耗大量的人力、物力、财力, 施工周期长, 受外界自然条件影响大, 诸多原因的影响常常导致工程的实际施工进度落后于计划进度。如何在预定的工期目标内完成工程项目, 降低工程成本, 提高经济效益, 已成为当前项目投资者和工程承包单位共同关心的问题。为此, 首先应对工程项目的工期目标进行仔细研究和论证, 确定科学合理的建设工期并制定施工进度计划, 同时还应根据进度计划对施工中所需的各种资源进行具体策划、统筹安排、合理使用、均衡消耗, 充分发挥有限资源的作用, 做好资源优化配置工作; 其次, 在施工进度计划实施过程中, 加强跟踪检查, 一旦发现因各种原因造成工期延误, 则可对原有网络计划关键线路上某些工作工时进行调整, 压缩这些工作的持续时间, 使工程按计划工期完成, 同时为赶工额外支付的费用最少。
下面, 通过工程案例来说明网络计划技术在优化资源配置—资源有限, 工期最短及利用工期—成本优化选择最佳赶工方案两个方面的应用。
资源优化—资源有限, 工期最短
资源是指为完成一项计划任务所需投入的人力、材料、机械设备和资金等。完成一项工程任务所需要的资源量基本上是不变的, 不可能通过资源优化将其减少。资源优化的目的是通过改变工作的开始时间和完成时间, 使资源按照时间的分布符合优化目标。在通常情况下,网络计划的资源优化分为两种, 即“资源有限, 工期最短”的优化和“工期固定, 资源均衡”的优化。所谓“资源有限, 工期最短”, 是指与施工进度计划相配套的资源需要量受到某种资源的限制, 若不增加资源数量会迫使工程的工期延长或不能进行, 此时在资源受到限制的条件下对施工进度计划进行调整。在调整计划过程中, 遵循有限资源在各工作之间合理分配的原则, 使各单位时间资源需求量均满足资源限量的要求, 以保证进度计划的顺利实施, 同时使工期延长最少, 优化示例Ⅰ如下:
已知某工程双代号网络计划如图Ⅰ—1 所示, 图中箭线上方数字为工作的资源强度, 箭线下方数字为工作的持续时间。假定资源限量Ra=12, 试对其进行“资源有限, 工期最短”的优化。
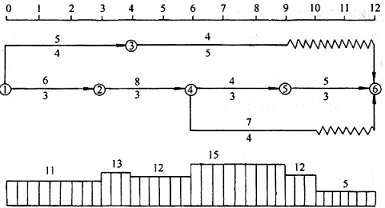
图Ⅰ—1 初始网络计划
该网络计划“资源有限, 工期最短”的优化可按以下步骤进行:
( 1) 计算网络计划每个时间单位的资源需用量, 绘出资源需用量动态曲线, 如图Ⅰ—1 下方曲线所示。
( 2) 从计划开始日期起, 经检查发现第二个时段[3, 4]存在资源冲突,即资源需用量超过资源限量, 故应首先调整该时段。
( 3) 在时段[3, 4]有工作1—3 和工作2—4 两项工作平行作业。对于两项平行作业的工作m 和工作n 来说, 为了降低相应时段的资源需用量, 考虑将工作n 安排在工作m 之后进行, 则网络计划的工期延长值为: △Tm,n=EFm—LSn, 其中EFm 为工作m 的最早完成时间, LSn 为工作n 的最迟开始时间, 利用以上公式计算△T 值, 其结果见表Ⅰ—1
表Ⅰ—1 △T 值计算表

由表Ⅰ—1 可知, △T1, 2=1 最小, 说明将第2 号工作( 工作2—4) 安排在第1 号工作( 工作1—3) 之后进行, 工期延长最短, 只延长1。因此, 将工作2—4 安排在工作1—3 之后进行, 调整后的网络计划如图Ⅰ—2 所示。
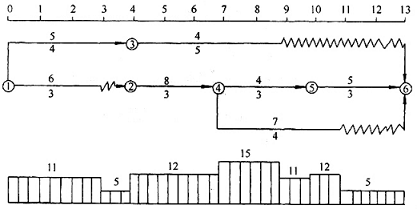
图Ⅰ—2 第一次调整后网络计划
( 4) 重新计算调整后的网络计划每个时间单位的资源需用量, 绘出资源需用量动态曲线, 如图Ⅰ—2 下方曲线所示。从图中可知, 在第四时段[7, 9]存在资源冲突, 故应调整该时段。
( 5) 在时段[7, 9]有工作3—6、工作4—5 和工作4—6 三项工作平行作业, 利用公式△Tm,n=EFm—LSn 计算△T 值, 其结果见表Ⅰ—2。
表Ⅰ—2 △T 值计算表
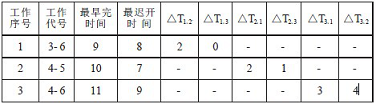
由表Ⅰ—2 可知, △T1, 3=0 最小, 说明将第3 号工作( 工作4—6) 安排在第1 号工作( 工作3—6) 之后进行, 工期不延长。因此, 将工作4—6 安排在工作3—6 之后进行, 调整后的网络计划如图Ⅰ—3 所示。
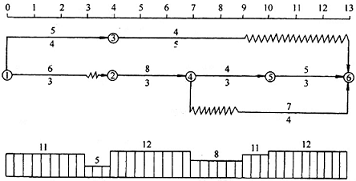
图Ⅰ—3 优化后的网络计划
( 6) 重新计算调整后的网络计划每个时间单位的资源需用量, 绘出资源需用量动态曲线, 如图Ⅰ—3 下方曲线所示。由于此时整个工期范围内的资源需用量均未超过资源限量, 故图Ⅰ—3 所示方案即为最优方案, 其最短工期为13。
工期—成本优化选择最佳赶工方案
工期—成本优化, 它是以满足工期要求的施工成本最低为目标的施工计划方案的调整过程。施工进度计划在执行过程中常因各种原因造成延误工时, 为了能按要求工期完成工程, 在执行后续计划时, 需要加快施工进度, 即赶工。通常可考虑逐次缩短那些有压缩可能且增加费用最低的关键工作的持续时间, 满足工期要求, 同时使计划安排相应的成本最低。在优化过程中, 应注意以下几点: 原关键路线上余下工作仍组成关键路线; 不能将关键工作压缩成非关键工作; 经压缩后的关键工作的工时必须不小于该工作的最短持续时间; 当出现多条关键线路时, 必须将各条关键线路的持续时间压缩同一数值, 否则不能有效地缩短工期, 优化示例Ⅱ如下:
某工程项目施工进度计划工作前锋线以后形成新的网络图如图Ⅱ—1 所示, 箭线上方字母为工序符号, 上方括号内数字为工序压缩一天需增加的费用( 千元/d) , 箭线下方数字为工序持续时间( d) , 下方括号内数字为工序最快持续时间( d) 。由于前期工作延误, 为了能按时完成工程任务, 后面工作需压缩工期2d, 试确定最佳赶工方案。
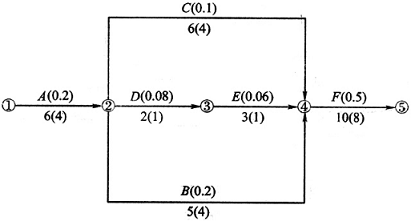
图Ⅱ—1
[解] 工期压缩目标为2 d, 应分成两个步骤完成:
( 1) 首先压缩工期1 d, 方案可采取: A 工序压缩1 d, 增加费用0.2千元; C 工序压缩1 d, 增加费用0.1 千元; F 工序压缩1 d, 增加费用0.5 千元。根据费用最小化原则选择压缩C 工序1 d, 形成如图Ⅱ—2网络图。
( 2) 工期压缩1 d 后的图Ⅱ—2 网络图中有3 条关键路线, 即A—C—F, A—D—E—F 及A—B—F。由于C、B 及DE 工序成平行作业工序, 单独压缩其中1 个工序作业时间, 工期不能缩短, 必须采用组合式压缩。压缩优化工期过程如表Ⅱ—1。
Ⅱ—1 压缩优化工期过程
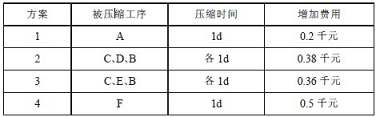
由表Ⅱ—1 得出结论, A 工序压缩1 d, 增加费用0.2 千元, 此方案最佳。
( 3) 综合( 1) 、( 2) 结论, 工期压缩目标为2 d 的最佳方案为: C 工序压缩1 d, A 工序压缩1 d, 增加的总费用为0.3 千元。
结束语
编制切实可行的网络计划, 同时在一定的约束条件下, 按既定目标对网络计划进行不断的检查、评价、调整和完善, 使其更有效地控制施工进度, 即优化网络计划。力求以最小的资源消耗取得最大的经济效益, 确保工程项目目标顺利实现。网络计划技术作为现代建筑企业管理中一项重要内容, 随着我国经济改革的深入和工程管理现代化的推进, 它在工程项目控制与管理中, 将发挥越来越大的作用。






