摘要:为解决建筑电气系统故障诊断和监测中高度依赖人工巡查和检测,自动化程度低下导致故障诊断滞后的问题,有必要研究以智能化的监测方法或手段诊断出故障位置,达到高效和经济的目的。本文以实际工程案例为依托,在研究建筑电气故障事故的监测基础上,以此为机器学习样本,提出基于BP神经网络法和ELM机器极限学习机法的建筑电气故障诊断方法。研究结果可为新建建筑或者老旧小区改造的建筑电气故障诊断和监测提供方法和案例。
关键词:故障诊断;BP神经网络法;建筑电气;监测方法;ELM极限学习机法
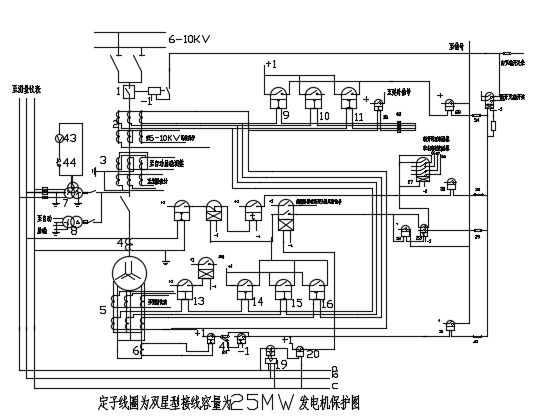
现代建筑是一个复杂的系统工程,包含了结构工程、给排水工程、电气工程等。由于智能建筑技术的发展和建筑使用者对建筑功能的多样化需求,不同的建筑物对建筑电气系统的功能要求也不一致,导致建筑电气系统也日益复杂化、多样化。依靠以往的人工巡查和检测,需要依赖于人工经验,自动化程度低,效率低下且浪费大量的人力,对于故障的诊断时效存在明显不足。为保证建筑电气能够安全运行,有必要研究以智能化的监测方法或手段诊断出故障位置,达到高效和经济的目的,预防由于建筑电气超负荷运转导致的短路、断电、电气火灾等事故,以保证建筑电气功能的实现和建筑使用者的安全,提供一个人性化的生活环境。
1建筑电气系统故障的监测
建筑电气系统主要分为供电系统和用电系统。其中供电系统是将电源输送至用电设备;用电系统又可以细分为弱电系统、照明系统和动力系统,弱点系统由消防报警系统、电话通讯系统和有线电视组成,动力系统是指将建筑电梯、给排水水泵以及通风空调功能设备等,照明系统是满足人们生产生活,提供光源和视觉环境的系统,主要为灯具照明。由上可知,建筑电气的故障分析受到多种因素的影响,目前尚未有一个适用于全面故障诊断的理论方法,但是对于一般的建筑电气故障可以根据以往的建筑监测检测中进行总结,并作为机器学习的样本。经过大量的工程总结,对建筑电气系统出现的故障进行监测,监测异常现象主要可以分为以下6类,如图1所示。从图1a中可以看出,A相发生单线接地故障时,其电压出现明显的下降,B相和C相的电压则相反,其电压幅值上升,但B相和C相的电流保持不变,而A相的电流激增;从图1b中可以看出,A相和B相发生短路事故时,两者的电压相位发生变化,电压线性发生畸变,在电流曲线上表现出激增,而C相的电压和电流均保持不变;从图1c中可以看出,A相和B相发生短路接地故障时,A相、B相和C相的电压出现畸变和激增,在电流上,A相、B相的电流明显增加而C相电流保持不变;从图1d中可以看出,A相、B相和C相均发生短路故障时,电压幅值明显下降,而电路则激增十几倍,出现此现象时,应立即断电否则会对电气设备产生不可逆的严重损害;从图1e中可以看出,A相发生单箱缺相故障后,它的电流值直降至0,电压也随之上升,而B相和C相的电压和电流保持不变;从图1f中可以看出,A相、B相和C相均发生断相故障时,三者的电流均直降至0,而电压仍维持在原先的水平。
2基于BP神经网络法的建筑电气故障诊断及实现
BP神经网络算法是在仿生学基础上发展出来的数学系统计算算法,它通过模拟生物的神经信号传递过程对输入信号进行学习训练,并不断地进行优化隐藏层的权函数,以达到理想的参数输出,为决策提供定量化和自动化计算的目的,它广泛应用于工程管理、图像优化、计算机学习以及人工智能等领域。在建筑电气领域,它可以应用于电气故障排查和诊断、优化电气线路,为建筑电气管理人员的决策提供依据。BP神经网络的基本原理如图2所示,它是正向学习的及其学习方法,其层次主要分为3层,分别为输入层、隐藏层(可以为多个层级,如图2中所示,有两层隐藏层)和输出层。输出层中包含了大量的训练样本,将其与训练集中的样本进行学习训练,即经过隐藏层的运算和传递,达到输出层,输出层参数结果与实际值进行对比,如果两者出现误差,则通过调整隐藏层的权函数值、阈值等,直到计算结果达到精度要求,即为期望的优化结果。对于图1中的输入层参数假设为x=[x1,x2,……xm],实际样本值为y=[y1,y2,……yn],各个隐藏层的权值函数如方程(1)、方程(2)所示。各个隐藏层的阈值可以用公式(3)、公式(4)所示。输出层参数结果与实际值的误差如公式(5)所示。对误差求偏导,将偏导赋值为零即为得到各层的阈值函数,如公式(6)、公式(7)所示。基于BP神经网络法建立建筑电气故障诊断模型,输入参数分别为故障发生后的三相电压值、三相电流值、三相电压畸变率和三相电流畸变率,对110个样本进行学习,采用120次的迭代,将训练目标误差设定为0.0035,得到诊断结果如图3所示。从图中可以看出,在110个样本中,12个样本点的误差偏离0,但误差范围在-1%~2%之间,得到的输出结果与预期符合程度较好。
3基于ELM极限学习机法的建筑电气故障诊断及实现
尽管BP神经网络法具有多隐藏层的结构,加大了诊断计算能力,但是也存在着一些明显的缺点,比如对学习率η值敏感,导致计算结果收敛慢或者不容易收敛。因此在基于BP神经网络算法的基础上发展出了ELM极限学习机法,它与BP神经网络算法最大的不同是在中间隐藏层中具有不固定的隐藏层神经元数目,在计算过程中可以不断修改隐藏层神经元的数目,以达到快速计算和全局最优搜寻的目的。同样地,在ELM极限学习机中,建立输入层与隐藏层之间的权值函数如方程(8)所示、建立隐藏层与输出层之前的权值函数如方程(9)所示。设定输入层参数假设为x=[x1,x2,……xm],实际样本值为y=[y1,y2,……yn],可以得到基于ELM极限学习机法的计算输出值,如方程(10)、方程(11)所示。法采用仿真软件建立建筑电气故障诊断模型,输入参数分别为故障发生后的三相电压值、三相电流值、三相电压畸变率和三相电流畸变率,对110个样本进行学习,采用120次的迭代,得到诊断结果如图4所示。从图中可以看出,在110个样本中,3个样本点的误差偏离0,比BP神经网络的计算误差大大减小,但误差范围在-8%~2%之间,得到的输出结果与预期符合程度较好。
4BP神经网络法与ELM极限学习机法的对比分析
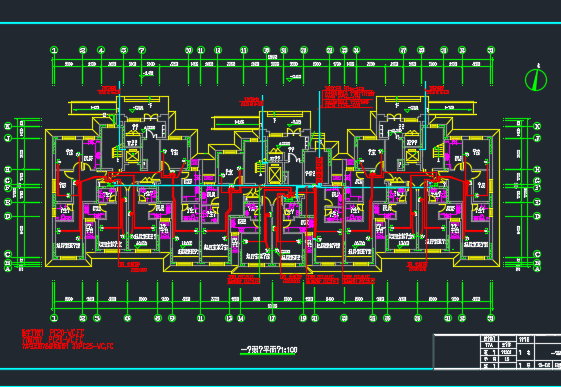
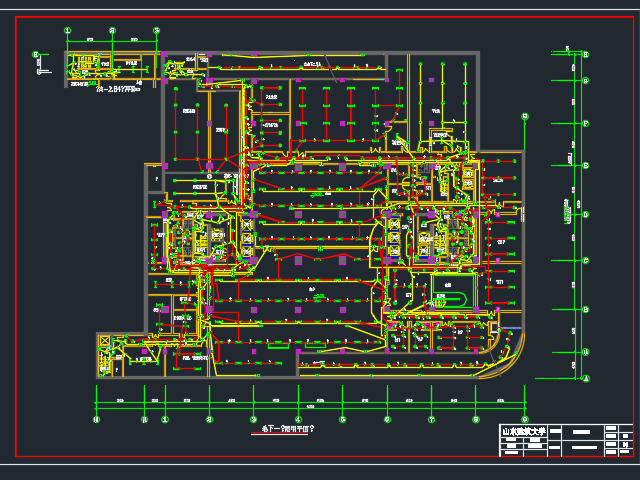
以内蒙古呼和浩特市某安置房小区一期为研究对象,小区位于城区东北角区域核心商圈范围,附近已有配套公用设施,交通便利。项目包含4栋住宅楼,均为混凝土框剪结构,楼栋地上建设15层,地下建设1层地下车库,小区现有住户130户,每户建筑面积约98m2,根据设计规范,每个楼栋内的电力设计负荷为15kW,使用三相线路进行供电,小区共配备了5台总配电箱。分别基于BP视神经网络法和ELM极限学习机法对工程实例的建筑电气故障建立仿真模型进行分析,得到仿真计算结果如表1所示。从表1中可以看出,基于BP视神经网络法在单相接地、单相缺相预测上存在较大的误差,而ELM极限学习法则在单相阶地。两相短路的预测上准确率相对较小;基于BP视神经网络法的故障平均预测准确率明显低于ELM极限学习法的故障平均预测准确率,BP视神经网络法的故障预测时间耗费0.475s,而于ELM极限学习法的故障预测时间耗费0.202s,后者比前者的计算效率提高约一倍,因此在建筑电气系统故障诊断中,可以优先选用ELM极限学习法
5结论
以内蒙古呼和浩特市某安置房小区一期为依托,在研究建筑电气故障事故的监测基础上,以此为机器学习样本,基于BP神经网络法和ELM机器极限学习机法对建筑电气故障进行诊断,得出以下几个结论:
5.1对建筑电气系统出现的故障进行监测,监测异常现象主要可以分为6类,即单相接地故障、两相短路接地故障、三相短路故障、两相短路故障、单相缺相故障、三相缺相故障。
5.2基于BP视神经网络法在单相接地、单相缺相预测上存在较大的误差,而ELM极限学习法则在单相阶地。两相短路的预测上准确率相对较小;基于BP视神经网络法的故障平均预测准确率明显低于ELM极限学习法的故障平均预测准确率,后者比前者的计算效率提高约一倍,因此在建筑电气系统故障诊断中,可以优先选用ELM极限学习法。