高斯-克吕格投影
1、高斯-克吕格简介
高斯-克吕格(Gauss-Kruger)投影简称“高斯投影”,又名"等角横切椭圆柱投影”,地球椭球面和平面间正形投影的一种。德国数学家、物理学家、天文学家高斯(Carl FriedrichGauss,1777一 1855)于十九世纪二十年代拟定,后经德国大地测量学家克吕格(Johannes Kruger,1857~1928)于 1912年对投影公式加以补充,故名。该投影按照投影带中央子午线投影为直线且长度不变和赤道投影为直线的条件,确定函数的形式,从而得到高斯一克吕格投影公式。投影后,除中央子午线和赤道为直线外, 其他子午线均为对称于中央子午线的曲线。设想用一个椭圆柱横切于椭球面上投影带的中央子午线,按上述投影条件,将中央子午线两侧一定经差范围内的椭球面正形投影于椭圆柱面。将椭圆柱面沿过南北极的母线剪开展平,即为高斯投影平面。取中央子午线与赤道交点的投影为原点,中央子午线的投影为纵坐标x轴,赤道的投影为横坐标y轴,构成高斯克吕格平面直角坐标系。
2、高斯-克吕格特性
(1)等角投影——投影前后的角度相等,但长度和面积有变形;
(2)等距投影——投影前后的长度相等,但角度和面积有变形;
(3)等积投影——投影前后的面积相等,但角度和长度有变形。
3、投影的基本概念
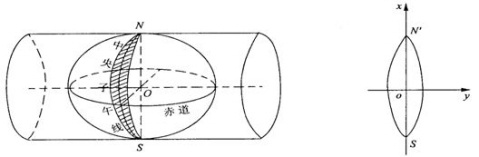
它是一种横轴等角切圆柱投影。它把地球视为球体,假想一个平面卷成一个横圆柱面并把它套在球体外面,使横轴圆柱的轴心通过球的中心,球面上一根子午线与横轴圆柱面相切。这样,该子午线在圆柱面上的投影为一直线,赤道面与圆柱面的交线是一条与该子午线投影垂直的直线。将横圆柱面展开成平面,由这两条正交直线就构成高斯-克吕格平面直角坐标系。为减少投影变形,高斯-克吕格投影分为3o带和6o带投影。
4、分带投影
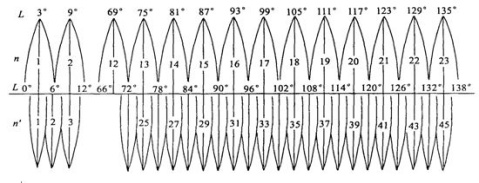
(1)高斯投影6度带:自0度子午线起每隔经差 自西向东分带,依次编号1,2,3,…。我国6度带中央子午线的经度,由75度起每隔6度而至135度,共计11带(13~23带),带号用n表示,中央子午线的经度用L表示,它们的关系是L=6n-3 ,如上图所示。
(2)高斯投影3度带:它的中央子午线一部分同6度带中央子午线重合,一部分同6度带的分界子午线重合,如用 n表示3度带的带号, 表示L带中央子午线经度,它们的关系L=3n。我国3度带共计22带(24~45带)。
5、高斯平面直角坐标系
在投影面上,中央子午线和赤道的投影都是直线,并且以中央子午线和赤道的交点o作为坐标原点,以中央子午线的投影为纵坐标x轴,以赤道的投影为横坐标y轴。
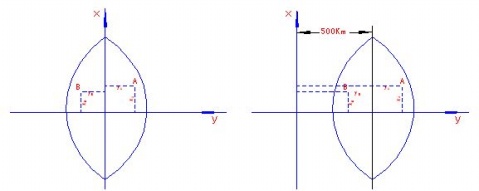
在我国 坐标都是正的, 坐标的最大值(在赤道上)约为330km。为了避免出现负的横坐标,可在横坐标上加上500 000m。此外还应在坐标前面再冠以带号。这种坐标称为国家统一坐标。
这也就是为什么在RTK测量中在输入投影参数时,Y坐标加常数增加了500 000m的原因。
6、高斯平面投影的特点
①中央子午线无变形;
②无角度变形,图形保持相似;
③离中央子午线越远,变形越大。
由此可见,在测量中,如果中央子午线输错了,投影的中央子午线就会编离实地坐标系正确的中央子午线,变形就越大,最终的结果就使用测量的误差更大。






