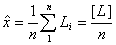首先从数学的角度阐述平差中产生的方程式数量、未知数数量问题,进而说明天然的平差模型无法得到唯一解这个结论,从而启发学生知道应该引入一定条件解决此问题,顺理成章引入最小二乘原理,并说明其含义及应用方法。
教学内容:
一、平差函数模型的方程式数量与未知数数量及解方程存在的问题
1.平差函数模型的方程式数量与未知数数量
通过前面的论述可知,如果只对几何模型中的必要元素进行观测,而没有多余观测,则在观测值之间不可能产生任何函数关系式,也不存在平差问题。只有在有了多余观测的情况下,才会产生平差问题。
例如为确定一个三角形的大小和形状,必要观测数为t=3,如果实际观测了一边三角(n=4),则存在一个多余观测(r=n-t=1)。现以一边和其中任意两个角作为一个组合来确定三角形的大小和形状,则有三种组合,由于观测值不可避免地含有偶然误差,三种组合所计算的结果将出现微小差别,这说明在具有多余观测的情况下,将无法唯一的确定模型的解。
从函数模型来考虑,由于存在一个多余观测,三个内角真值之间就存在一个条件方程,即:
![]()
考虑到![]() ,代入上式得
,代入上式得
![]() (2-4-1)
(2-4-1)
式中
![]() (2-4-2)
(2-4-2)
称为条件方程的闭合差或常数项,它是可以根据观测值计算出来的。由于观测值的真值不知道,所以真误差![]() 是未知量。
是未知量。
2.存在的问题及解决办法---引入最小二乘原理
要根据(2-4-1)式确定真误差的值,显然其解是不唯一的。要确定满足函数模型的唯一的一组解,如果不另外附加一定的约束条件,那是不可能的。到底应该采用什么样的约束条件,才能使模型得到一组具有最佳性质的解呢?
在测量工作及其它科学工程领域,应用最早也最广泛的就是所谓的“最小二乘准则”:
![]() (2-4-3)
(2-4-3)
二、最小二乘原理含义及应用方法说明
在满足最小二乘准则下求得的真误差称为![]() 估值,用
估值,用![]() 表示,测量工作中习惯上用符号
表示,测量工作中习惯上用符号![]() 代替
代替![]() ,因此最小二乘准则常表达为:
,因此最小二乘准则常表达为:
![]() (2-4-4)
(2-4-4)
由于根据最小二乘准则可以求得真误差估值![]() ,也就可以求得观测值的估值,其计算公式为
,也就可以求得观测值的估值,其计算公式为
![]() (2-4-5)
(2-4-5)
式中![]() 称为观测值的改正数,
称为观测值的改正数,![]() 称为观测值
称为观测值![]() 的估值,或平差值、最或然值。
的估值,或平差值、最或然值。
应用最小二乘准则,并不需要知道观测向量属于什么概率分布,只需要知道它的先验权阵![]() 就可以了。
就可以了。
当![]() 为非对角阵,表示观测值相关,按
为非对角阵,表示观测值相关,按![]() 进行的平差称为相关观测平差。
进行的平差称为相关观测平差。
当![]() 为对角阵,表示观测值不相关,此时最小二乘准则可表示为纯量形式,即:
为对角阵,表示观测值不相关,此时最小二乘准则可表示为纯量形式,即:
![]() (2-4-6)
(2-4-6)
特别地,当观测值不相关且等精度时,权阵![]() 为单位阵,此时最小二乘准则可表示为
为单位阵,此时最小二乘准则可表示为
![]() (2-4-7)
(2-4-7)
其实,估计的准则有许多种,最小二乘准则是其中的一种,还有一种常用的估计叫做最大似然估计,这种估计要求事先知道观测量的概率分布函数。一般认为测量观测值向量是服从正态分布的随机变量,其概率分布密度函数为
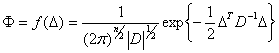 (2-4-8)
(2-4-8)
所谓极大似然估计,就是要在概率分布密度函数达到极大的条件下来对真误差![]() 进行估计。显然,当
进行估计。显然,当![]() 达到极小时,概率分布密度函数可取得极大值,仍用
达到极小时,概率分布密度函数可取得极大值,仍用![]() 表示对
表示对![]() 的估计结果,即要求:
的估计结果,即要求:
![]()
相当于
![]()
显然,当观测向量服从正态分布时,极大似然估计与最小二乘估计的结果是一致的。
三、最小二乘原理应用举例
例[2-2] 设对某物理量![]() 进行了
进行了![]() 次同精度独立观测,得观测值
次同精度独立观测,得观测值![]() ,试按最小二乘准则求该量的估计值。
,试按最小二乘准则求该量的估计值。
解:设该量的估计值为![]() ,则有
,则有
![]()
![]()
写成矩阵形式
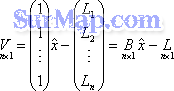
按最小二乘准则,要求
![]()
将上式对![]() 取一阶导数,并令其为零,得
取一阶导数,并令其为零,得

将![]() 代入上式得
代入上式得
![]()
有此解得