复化辛卜生公式及公路中线坐标计算中的应用

在公路中线坐标计算中，我们通常采用切线支距公式来计算曲线上各点的坐标。但当在不同的曲线上计算时就需用不同的计算公式，这为计算也带来不便。在设有缓和曲线的圆曲线半径较小或是卵形曲线上的坐标计算时，如公式选用不当就会出现较大计算误差，即便是能对切线支距公式进行多项展开，也会增加计算的难度。而用复化辛卜生公式不仅能解决不同曲线线型或直线上的坐标计算问题，而且用复化辛卜生公式计算完全是可逆的（即：可顺前进方向也可逆向计算），尤其在计算第二缓和曲线和卵形曲线时显得尤为方便。

用辛卜生公式计算坐标的精度可由人为或程序自行判断，其计算结果完全能保证坐标计算的精度要求。因此，可以说复化辛卜生公式是一个计算公路中线坐标的万能公式。下面本人就该公式在公路中线坐标计算中的具体应用进行实例解析。

一、复化辛卜生公式

式中：

H=（Z_i－Z_A）/n

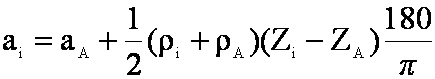(公式2)

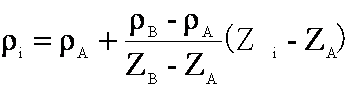(公式3)

Zi­­—待求点桩号

Z_A—曲线元起点桩号

Z_B—曲线元终点桩号

ρ_A—曲线元起点曲率

ρ_B—曲线元终点曲率

a _i曲线上任意一点处切线方位角的计算方法有以下三种方法：

1．利用公式（3）求得曲率代入公式（2）计算

2．利用曲线元上已知起点和终点曲率用内插法求得曲率代入公式（2）计算

3．利用切线角公式计算

二、算例

例：已知雅（安）攀（枝花）高速公路西昌西宁立交A匝道一卵形曲线（卵形曲线相关参数见图一，其计算略。），相关设计数据见下表。现用辛卜生公式来计算卵形曲线中桩坐标。

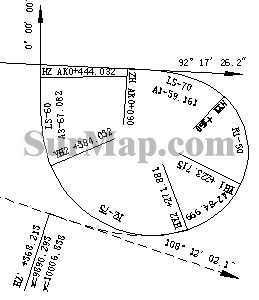
图一

已知相关设计数据见下表：

主点   桩号	坐 标   （m）		切线方位角   （θ）
	X	Y	° ’ ”
ZH   AK0+090	9987.403	10059.378	92 17 26.2
HY1   AK0+160	9968.981	10125.341	132 23 51.6
YH1   AK0+223.715	9910.603	10136.791	205 24 33.6
HY2   AK0+271.881	9880.438	10100.904	251 24 18.5
YH2   AK0+384.032	9922.316	10007.909	337 04 54.2
HZ   AK0+444.032	9981.363	10000.000	0 00 00

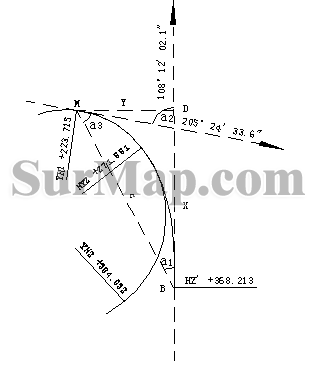
（一）由+271.881推算Zi=+223.715的坐标，n取2等分

用公式(3)、公式（2）计算+247.798处曲线及方位角:

ρ_+247.798=1÷75+(1÷50-1÷75)(247.798-271.881) ÷(223.715-271.881)

=0.01666666666666667

a_+247.798=71°24’18.5” +(0.016666667+1÷75)(247.798-271.881)×180÷π÷2

=50°42’26.37”

其它各点依次代入公式计算，结果见下表:

曲率及切线方位角计算表

桩号	n等分点处曲线曲率		n等分点处   切线方位角 ° ’ ”	2n等分点处曲线曲率		2n等分点处   切线方位角 ° ’ ”
	公式(3)   计 算	内插法   计 算		公式(3)   计 算	内插法   计 算
+271.881	0.013333333=1/75		71 24 18.5
+259.840				0.015	0.015	61 37 52.2
+247.798	0.016666667	0.016666667	50 42 26.4
+235.757				0.018333333	0.0183333333	38 38 0.96
+223.715	0.02=1/50		25 24 36

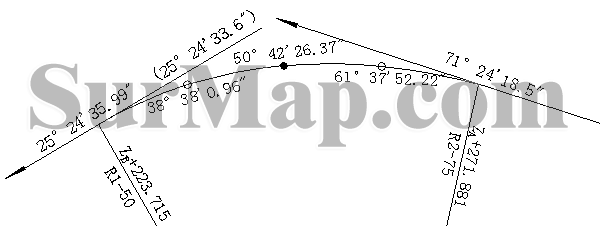
切线方位角图示1

将计算出的数据代入公式（1）求得+223.715中桩坐标如下：

X=9880.438+(271.881-223.715)÷2÷6×(cos71°24’18.5”+4(cos61°37’52.22”+cos38°38’0.96”)

+2cos50°42’26.37”+ cos25°24’35.99”)

=9910.5975 (设计值：9910.603)

Y=10100.904+(223.715-271.881)÷2÷6×(sin71°24’18.5”+4(sin61°37’52.22”+sin38°38’0.96”)

+2sin50°42’26.37”+ sin25°24’35.99”)

=10136.7945 (设计值：10136.791)

（二）由+223.715推算Zi=+271.881的坐标，n取2等分

用公式(3)计算+247.798处曲线及方位角:

ρ_+247.798=1÷50+(1÷75-1÷50)(247.798-223.715)÷(271.881-223.715)

=.01666666666666667

a_+247.798=205°24’33.6”+ (0.016666667+1÷50)(247.798-223.715)×180÷π÷2

=230°42’23.98”

其它各点依次代入公式计算，结果见下表:

曲率及切线方位角计算表

桩号	n等分点处曲线曲率		n等分点处   切线方位角 ° ’ ”	2n等分点处曲线曲率		2n等分点处   切线方位角 ° ’ ”
	公式(3)   计 算	内插法   计 算		公式(3)   计 算	内插法   计 算
+223.715	0.02=1/50		205 24 33.6
+235.757				0.018333333	0.0183333333	218 37 58.6
+247.798	0.016666666	0.016666666	230 42 24.0
+259.840				0.015	0.015	241 37 49.8
+271.881	0.013333333=1/75		251 24 18.5

切线方位角图示2

X=9910.603+(271.881-223.715)÷2÷6×(cos205°24’33.6”+4(cos218°37’58.87”+cos241°37’49.83”)

+2cos230°42’23.98”+ cos251°24’16.11”)

=9880.4431 (设计值：9880.438)

Y=10136.791+(271.881-223.715)÷2÷6×(sin205°24’33.6”+4(sin218°37’58.87”+sin241°37’49.83”)

+2sin230°42’23.98”+ sin251°24’16.11”)

=10100.9008 (设计值：10100.904)

由上可知，利用复化辛卜生公式计算路线坐标时可顺向或逆向计算。

（三）前面正、反向的计算均是从卵形曲线的部分推算的，现在我们从卵形曲线所在完整缓和曲线的起点HZ’=+368.213点来推算终点+223.715和中间点+271.881.

a_i=a_A-90L²÷(πRL_S)公式(4)

1.计算Zi=+223.715中桩坐标

曲线元上等分点曲率及切线方位角计算表(n取4等分)

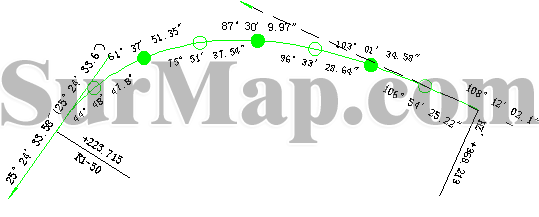
切线方位角图示3

X=9890.293+(368.213-223.715)÷4÷6×(cos108°12’02.1”+4(cos106°54’25.22”+cos96°33’28.64”

+ cos75°51’37.54”+ cos44°48’47.8”)+2(cos103°01’34.58”+ cos87°30’9.97” +cos61°37’51.35”)

+ cos25°24’33.58”)

=9910.5963 (设计值：9910.603)

Y=10006.838+ (368.213-223.715)÷4÷6×(sin108°12’02.1”+4(sin106°54’25.22”+sin96°33’28.64”

+ sin75°51’37.54”+ sin44°48’47.8”)+2(sin103°01’34.58”+ sin87°30’9.97” +sin61°37’51.35”)

+ sin25°24’33.58”)

=10136.7925 (设计值：10136.791)

2.计算zi=+271.881中桩坐标

曲线元上等分点曲率及切线方位角计算表(n取4等分)

桩号	n等分点处   曲线曲率	n等分点处   切线方位角 ° ’ ”		2n等分点处曲线曲率	2n等分点处   切线方位角 ° ’ ”
	内插法   计 算	公式(2)计算	公式(4)计算	内插法   计 算	公式(2)计算	公式(4)计算
+368.213	0	108 12 02.1
+356.172				0.001666667		107 37 32.49
+344.130	0.003333333		105 54 02.97
+332.089				0.005		103 01 34.58
+320.047	0.006666667		99 00 05.6
+308.006				0.008333333		93 49 38.42
+295.964	0.01		87 30 09.97
+283.923				0.011666667		80 01 44.02
+271.881	0.013333333=1/75		71 24 16.09
+223.715	0.02=1/50	25 24 33.58	25 24 33.58

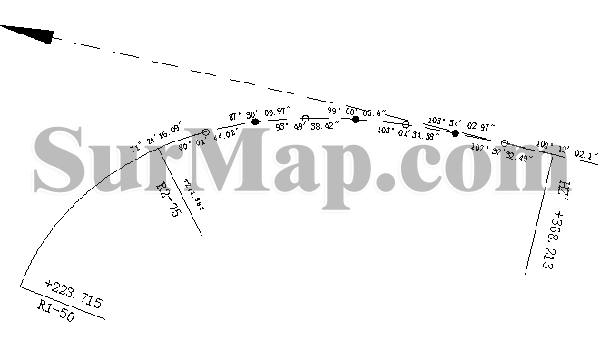
切线方位角图示4

X=9890.293+(368.213-271.881)÷4÷6×(cos108°12’2.1”+4(cos107°37’32.49”+cos103°01’34.58”

+ cos93°49’38.42”+ cos80°01’44.02”)+2(cos105°54’02..97”+ cos99°00’05.6” +cos87°30’09.97”)

+ cos71°24’16.09”)

=9880.4416 (设计值：9880.438)

Y=10006.838+ (368.213-271.881)÷4÷6×(sin108°12’2.1”+4(sin107°37’32.49”+sin103°01’34.58”

+ sin93°49’38.42”+ sin80°01’44.02”)+2(sin105°54’02.97”+ sin99°00’05.6” +sin87°30’09.97”)

+ sin71°24’16.09”)

=10100.9008 (设计值：10100.904)

由此我们不难看出，利用复化辛卜生公式计算公路中桩坐标不仅顺逆向很方便，而且可从中任取一段进行计算。而计算中的关键是计算各等分点处的切线方位角，同时应分清n与2n等分点，注意不要混淆。对于n的取值，从上我们可以看出：对一般缓和曲线取2-3即可，对卵形曲线视推算基准点而言不少于4。

其它如圆曲线、直线等中桩坐标的计算方法是一样的，在此就不一一简述。

桩 号	n等分点处   曲线曲率		n等分点处   切线方位角 ° ’ ”		2n等分点处曲线曲率		2n等分点处   切线方位角 ° ’ ”
	公式(3)   计 算	内插法   计 算	公式(2)计算	公式(4)计算	公式(3)   计 算	内插法   计 算	公式(2)计算	公式(4)计算
+368.213	0		108 12 02.1
+350.151					0.0025	0.0025	106 54 25.16	106 54 25.22
+332.089	0.005	0.005	103 01 34.33	103 01 34.58
+314.026					0.0075	0.0075	96 33 28.83	96 33 28.64
+295.964	0.01	0.01	87 30 09.97	87 30 9.97
+277.902					0.0125	0.0125	75 51 37.22	75 51 37.54
+259.840	0.015	0.015	61 37 50.58	61 37 51.35
+241.777					0.0175	0.0175	44 48 48.25	44 48 47.8
+223.715	0.02=1/50		25 24 33.58	25 24 33.58