一、缓和曲线
缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用
1)便于驾驶员操纵方向盘
2)乘客的舒适与稳定,减小离心力变化
3)满足超高、加宽缓和段的过渡,利于平稳行车
4)与圆曲线配合得当,增加线形美观
2.缓和曲线的性质
为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)
ρ=C/s
C=A2
由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程
即用回旋线作为缓和曲线的数学模型。
令:ρ=R,lh=s 则 lh=A2/R
4.缓和曲线最小长度
缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。缓和曲线的最小长度应按发挥其作用的要求来确定:
1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。a1=0,a2=v2/ρ,as=Δa/t≤0.6
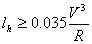
2)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)
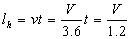
3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度
超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
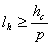
4)从视觉上应有平顺感的要求计算缓和曲线最小长度
缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算
1)回旋线切线角
(1)缓和曲线上任意点的切线角
缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
βx=s2/2Rlh
(2)缓和曲线的总切线角
β=lh/2R.180/л
2)缓和曲线直角坐标
任意一点P处取一微分弧段ds,其所对应的中心角为dβx
dx=dscosβx
dy=dssinβx
3)缓和曲线常数
(1)主曲线的内移值p及切线增长值q
内移值:p=Yh-R(1-cosβh)=lh2/24R
切线增长值:q=Xh-Rsinβh=lh/2-lh3/240R2
(2)缓和曲线的总偏角及总弦长
总偏角:βh=lh/2R
总弦长:Ch=lh-lh3/90R2
O为圆曲线的圆心,圆曲线所对圆心角 (等于公路偏角
(等于公路偏角 )。当插入缓和曲线后,可以看作是原来半径为R+△R的圆曲线向内移动了△R距离,因此设置缓和曲线后的圆曲线半径为R。
)。当插入缓和曲线后,可以看作是原来半径为R+△R的圆曲线向内移动了△R距离,因此设置缓和曲线后的圆曲线半径为R。
当设置缓和曲线后,圆曲线所对圆心角也相应减小,减小后的圆心角等于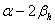 ,因而设置缓和曲线的可能条件为:
,因而设置缓和曲线的可能条件为: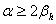 ,当
,当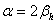 时,两条缓和曲线在弯道中央直接相接,没有圆曲线段,形成了一条连续的缓和曲线。当
时,两条缓和曲线在弯道中央直接相接,没有圆曲线段,形成了一条连续的缓和曲线。当 时,则不能设置所规定的缓和曲线,这时必须缩短缓和曲线长度或增大圆曲线半径。
时,则不能设置所规定的缓和曲线,这时必须缩短缓和曲线长度或增大圆曲线半径。
4)缓和曲线要素计算
《公路工程技术标准》规定,当R<R免时,必须设置缓和曲线。
切线长
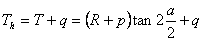
外距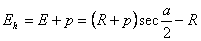
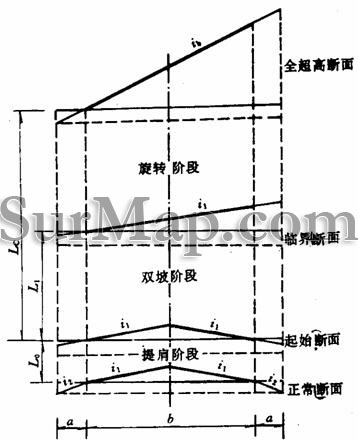
曲线长 圆曲线长 切线差 平曲线五个基本桩号: ZH——HY——QZ——YH——HZ 二、超高缓和段 1.超高缓和段的过渡形式 从直线上的双向路拱横坡,过渡到圆曲线上具有超高横坡度的单向坡断面,这一变化段称为超高缓和段。 1)无中央分隔带的公路 (1)绕路面内边缘旋转 先将外侧车道绕路中线旋转,待达到与内侧撤到构成单向横坡后,整个断面再绕未加宽前的内侧车道边缘旋转,直至超高横坡值。 适用:一般用于新建工程及以路肩边缘为设计高程的改建公路。 (2)绕路面中心线旋转 先将外侧车道绕路中线旋转,待达到与内侧车道构成单向横坡,整个断面一同绕路中线旋转,直至超高横坡值。 适用:一般用于改建工程,尤其是以路中心标高作为设计标高的情况。 (3)绕路面外侧边缘旋转 整个断面再绕未加宽前的外侧车道边缘旋转,直至超高横坡值。 适用:一般用于挖方的工程。 2)有中央分隔带的公路 (1)绕中间带的中心线旋转 先将外侧车道绕中间带的中心线旋转,待达到与内侧行车道构成单向横坡后,整个断面一同绕中心线旋转,直至超高横坡值。此时中央分隔带呈倾斜状。 (2)绕中央分隔带两侧边缘旋转 将两侧行车道分别绕中央分隔带边缘旋转,使之各自成为独立的单向超高断面。中央分隔带形状保持不变。 (3)绕各自行车道中线旋转 将两侧行车道分别绕各自的中线旋转,使之各自成为独立的单向超高断面。此时中央分隔带两边缘分别升高与降低而成为倾斜断面。 2.超高缓和段的构成 路面在缓和段上要经过准备阶段、双坡阶段和旋转阶段等三个阶段,才能从正常路过渡到圆曲线上的全超高断面。 (1)准备阶段 准备阶段也叫做提肩。在进入超高缓和段之前的L0=1~2m范围内,把路肩横坡抬高到与路面相同的横坡,即使路基顶面变成简单的双向横坡。 (2)双坡阶段 先保持路面内侧不动,外侧绕路中线向上旋转到与内侧同坡,这一过程成为双坡阶段。其所需要的长度即为双坡阶段长度L1。 图超高的构成 (3)旋转阶段 当外侧路面变成与内侧相同的单向倾横坡后,路面保持内侧边缘线不动,整个路面绕内边缘线向上旋转,直到缓和段终点。其所需要的长度即为旋转阶段长度L2。 3.全超高断面全超高值的计算 超高值就是指设置超高后路中线、路面边缘及路肩边缘对路基设计高程的高差。 路基设计高程一般是指路肩边缘的高程,在设置超高 、加宽路段,为未超高、加宽前的路肩边缘的高程。 直线段及不设超高、加宽的平曲线上的标准横断面中,路中线与设计高程的高差为h中: 绕路面内边缘旋转的超高值计算: 圆曲线段的全超高断面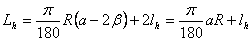
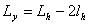
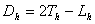
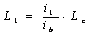
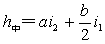
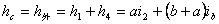
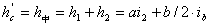
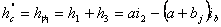
圆曲线上任一点相应的超高值都相等。
4.超高缓和段长度
超高缓和段必须有一定的长度。
超高渐变率:在超高缓和段上由于路基抬高,外侧路缘纵坡较原设计纵坡增加了一个附加纵坡。
绕路面内边缘旋转:路面外缘最大抬高值h=bib Lc=h/p=bib/p
5.超高缓和段上超高值的计算
超高缓和段的渐变是按路面外边缘线相对与设计高程的高差值随离开缓和段起点的距离成正比例增加的规律进行的,而路中线及路面内边缘线随之也做相应地变化。
由于超高渐变过程是经过三个阶段完成的。
(1)起始断面
经过提肩,路肩与路面相同横坡度的双坡断面。
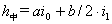
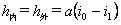
(2)双坡断面(x≤L1)
双坡断面就是指双坡阶段内任一点的断面,即从超高缓和起点至路面外侧变成与内侧相同坡度这一阶段内的断面。
则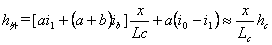
在双坡阶段中,路中线是保持不变: 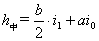
路面内侧的横坡保持不变,但当路面设置加宽时,路面及路肩边缘则随路面加宽值的渐变而作相应地变化。
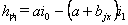
(3)旋转断面(x≥L1)
设旋转阶段中任一点离开缓和曲线起点地距离为x(x>L1),其路面横坡度为Ix,在超高缓和段上,超高坡度是由零按直线比例增加到设计超高坡度Ib值的,故
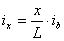
可得旋转阶段上的超高值计算公式如下:
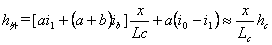
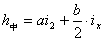
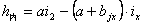
三、加宽缓和段
1.加宽缓和段长度计算
路面在圆曲线上设置加宽时,其宽度比直线段上大。为避免路面宽度从直线段上的正常宽度到圆曲线段的加宽断面的突变,在直线和圆曲线之间应设置一段路面宽度的渐变段。
(1)路线设置缓和曲线或超高缓和段时,加宽缓和段长度采用与缓和曲线或超高缓和段长度相同的值,,以尽量减少公路几何形状的变更次数。
(2)不设缓和曲线或超高缓和段时。加宽缓和段长度应按渐变率为1:15且长度不小于20m的要求设置,且取5米的整数倍。
2.加宽值的计算
(1)二、三、四级公路的加宽缓和段
加宽缓和段上任一点的加宽值bjx,与该点到加宽缓和段起点的距离Lx,同加宽缓和段全长Lj的比值成正比,即
Bjx=Lx/Lj.bj
(2)高等级公路加宽缓和
高速公路、一级公路以及对路容有要求的二级公路,设置加宽缓和段时,为使路面加宽后的边缘圆滑、适顺,采用高次抛物线的形式过渡;
Bjx=(4K3-3K4)*bj
(3)一、二级公路的近郊的路段、桥梁、高架桥、挡土墙、隧道及设置各种安全防护设施的路段,也可采用插入回旋线的方法。






