【摘 要】 本文提出了卵形曲线中缓和曲线段上点位坐标计算方案,推导了其计算过程及公式,并附实例。对始于高等级道路的平面卵形 曲线的测设有重要的指导作用。
高等级公路,特别是高速公路的平面线形设计形式很多,但归根结底,它们都由直线、圆和缓和曲线 ( 我国《公路路线设计规范》中规定回旋线或称菲涅尔螺旋线为缓和曲线线形 ) 等公路平面线形要素组合而成。各种平面线形设计形式,如基本形、卵形、 S 形、 C 形等等,对 高速公路更加适应汽车转弯时的行车轨迹,消除曲率突变,增进线形美观及行车舒适感、安 全感都有极其重要的意义,但同时,也使曲线计算及野外测设更为复杂。本文针对在高速公路设计实际中出现的卵形曲线,推导了缓和曲线段点位坐标计算方法及公式,为现场测设人员提供了有效的计算方案和测设指导。
一、回旋线的基本特征及坐标计算
回旋线上,任意一点的曲率半径 ρ 与该点至曲线起点的曲线长 l 之积为一常数 ( 图 1) 即
ρl =A2
(1)
或
![]()
式中, A 2 为回旋曲线常数,表征回旋曲线曲率变化缓急程度的量,称 A 为回旋曲线参数。
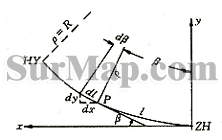
图 1
1. 回旋曲线上任意一点坐标计算
由图 1( 曲线右旋 ) ,取回旋线的起始点 ZH 处的切线方向为 x 轴,法线方向为 y 轴,任意一点的 切线方向方位角为缓和曲线角 β 。在缓和曲线上对任意一点 P 取微分
dl=ρdβ
dx=dlcosβ
dy=dlsinβ
考虑式 (1) 对 β 或 l 在区间 [0 , β ]或 [0 , l ]上积分后有下列关系式成立
l 2 = 2A 2 β
(2)
![]()
(3)
![]()
(4)
或者
![]()
(5)
![]()
(6)
对于公路平面线形的基本形,其缓和曲线始于直线终于圆曲线,故缓和曲线的曲率半径 ρ 变化于 ∞ ~ R ( 圆曲半径 ) 。设缓和曲线段长度为 ls , 则
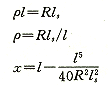
(7)
![]()
(8)
2. 回旋线的几何要素
见图 1 ,回旋线的几何要素计算公式如下:任意点 P 处的曲率半径 ( 由式 (1) 和式 (2))
![]()
(9)
P 点的回旋曲线长
![]()
(10)
P 点的缓和曲线角 ( 切线方位角,由 (9) 式 )
![]()
(11)
上面导出了当参数分别为 β 和 l 时的右旋缓和曲线上任一点的坐标和几何要素公式。显然,缓和曲线左旋时 ( 图 2) ,与右旋相比, x 坐标公式一致,而 y 、 β 反号。若令 sign=±1 ,缓和曲线右旋时取 sign=1 ,左旋时取 sign=-1 ,则坐标和方位角等符号量可统一 表示为:
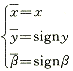
(12)

图 2
3. 回旋曲线的基本特征
1. 几何特性。回旋曲线随着曲线长度的增加,曲率按线性函数增加。起点处 l =0 ,曲率 l /ρ = 0 ,终点处 l =ls ,曲率 l /p =常数。
2. 相似性。回旋曲线的形状只有一种,回旋曲线参数 A 即为放大系数。
二、卵形曲线形式及其缓和曲线段坐标计算
按直线 - 缓和曲线 (A1)- 圆曲线 (R1)- 缓和曲线 - 圆曲线 (R2)- 缓和曲线 (A2)- 直线的顺序组合构成的平面线形形式 (R1≠R2) ,称为卵形曲线 ( 图 3) 。卵形曲线中,显然圆曲线 - 缓和曲线 - 圆曲线段的缓和曲线坐标计算是新的课 题,它成为整个卵形曲线计算的瓶颈。解决了这个问题,其他平面线形形式的曲线坐标计算 也就迎刃而解了。
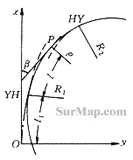
图 3
解决问题的关键在于对两圆曲线之间的缓和曲线的正确认识: (1) 两不等圆曲线之间的缓和 曲线仍是回旋线; (2) 该回旋线是没有起点 (ρ = 0) 的回旋线段。
于是,解决问题的方案是:第一,仍须确定哪端为回旋曲线的起点 (ρ = 0) 端;第二,假定缓和曲线起点而套用平面曲线基本形计算回旋曲线任意一点坐标及其方位角;第三,坐标变换为大地 ( 或施工区 ) 坐标形式,而这正是高效测设曲线的现代发展所需要的坐标形式。
我们知道,回旋曲线起点处曲率半径 ρ =∞ ,随着离曲线起点的曲线长度增加,曲率半径由大变小。因此,卵形曲线两圆之间回旋线的起点必在相接圆半径较大的圆曲线那一端。由此再确定回旋线的右或左旋形式以确定独立坐标公式 (sign 的值 ) 的使用。根据回旋线上特征点的已知大地坐标和独立坐标,可计算出坐标变换参数,从而得到回旋线上任意一点的大地坐标及其切向、法向方位角。
以图 3 为例,因为 R 1 >R2 ,可见回旋线的起点在 R 1 圆曲线的那一端,显然,该回旋线右旋。设回旋曲线起点为 O ,起点处切线方向为 x 轴,法线方向为 y 轴,建立独立坐标系。
O-YH 弧长: l 1 = A 2 /R1
O-HY 弧长: ls =l1+l0 = A 2 /R2
这里, l 0 =lYH-HY 为缓和曲线段长度。
缓和曲线上任意点 P 至起点 O 的弧长为
l′ = l 1 +l
这里, l 为 P 至圆缓点 YH 的弧长。
将 l 1 ,ls,l′ 分别替代 l 代入式 (7) 、式 (8) 得到圆缓点 YH 、缓圆点 HY 、任意点 P 独立坐 标系坐标 xYH ,yYH,xHY,yHY,xP,yP( 注意,计算时式中 R = R 2 ) 。
设独立坐标系 xOy 原点 O 的大地坐标为 (X0,Y0) , x 轴的大地方位角为 α 0 ,由 YH 、 HY 点的大地坐标和独立坐标可分别反算直线 YH-HY 的坐标方位角 α 1 ,α2 ,则
α 0 =α1-α2
(13)
于是,独立坐标系中任意一点 P (x,y) 的大地坐标 X , Y 为
X = X 0 +xcosα0-ysinα0
(14)
Y = Y 0 +xsinα0+ycosα0
(15)
这里, X 0 ,Y0 可由点 YH 或 HY 已知坐标数据 ( 大地、独立 ) 用上两式求得。
P 点切线大地方位角
α =α0+signβ
(16)
法线大地方位角
τ = (α-sign90)±180
(17)
三、算 例
广东某高速公路一段卵形曲线设计数据的特征点大地坐标见表 1 ,缓和曲线参数 A = 30 0 ,缓和曲线长度 l 0 =157.50 m ,两相接圆曲半径见图 4 。求缓和曲线内两里程桩号点的大地坐标及法向方位角。
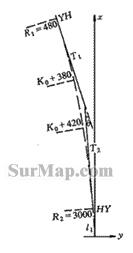
图 4
表 1 部分设计数据
|
点 号 )/( 里程桩号 )/(X/m)/(Y / m)/( 其他数据 |
|
圆缓点 (YH))/(K0+327.43)/(3 961.506)/(4 033.679)/(T1=59.95 |
|
交 点 (JD))/(K0+387.38)/(3 998.132)/(3 986.223)/(T2=97.98 |
|
缓圆点 (HY))/(K0+484.93)/(4 071.589)/(3 921.382)/(θ = 10°54′13″ |
简要计算如下:
因 R 2 >R1 ,可见回旋线起点在 R 2 端且左旋 (sign=-1) ,建立独立坐标系如图 4 。则
l 1 =A2/R2=30 m
ls=l1+l0=A2/R1 = 187.50 m
由此代入式 (7) 、式 (8) 并注意到 R = R 1 =480 得 HY , YH 点独立坐标为
![]()
由直线 HY-YH 的大地方位角 α 1 和独立方位角 α 2 得独立坐标轴 x 的大地方位角
α =α1-α2 = 138°51′05″
则
X 0 = 4 094.145 Y 0 = 3 901.605
于是缓和曲线上点 K 0 +420 处、 K 0 +380 处坐标与方位角数据可得
K 0 +420 : (l′=l1+484.93-420=94.93)
x =94.906 y =-1.584 β = 2°52′06″
X =4 023.723 Y =3 965.247 τ = 45°58′59″
K 0 +380 : (l′=l1+484.93-380=134.93)
x =134.792 y =-4.546 β = 5°47′43″
X =3 995.637 Y =3 993.723 τ = 43°03′22″
四、结束语
卵形曲线中两圆曲之间的缓和曲线段是螺旋回旋线不含起点的一部分。其上任意点的坐标计 算仍可套用平面线形基本形中的缓和曲线点的坐标公式。本文给出的卵形曲线中缓和曲线段 任一点的坐标特别是大地坐标及其法向方位角的解算方案及公式,既解决了测设数据的数值 计算问题,又适应了野外测设使用大地坐标设站灵活性强、效率高、节省外业工作量的现代 发展趋势。使用可编程的便携机非常方便快捷。






