1 绪论
坐标系统的选择对一项工程来说是一项首先必须进行的工作,同时坐标系统选择的适当与否关系到整个工程的质量问题,因此对坐标系统的研究是一项非常重要和必须的工作。
我国《规范》规定:所有国家的大地点均按高斯正形投影计算其在![]() 带内的平面直角坐标……。在1:1万和更大比例尺测图的地区,还应加算其在
带内的平面直角坐标……。在1:1万和更大比例尺测图的地区,还应加算其在![]() 带内的直角坐标系。我们通常将这种控制点在
带内的直角坐标系。我们通常将这种控制点在![]() 带或
带或![]() 带内的坐标系称为国家统一坐标系统。
带内的坐标系称为国家统一坐标系统。
在实际应用中,国家统一坐标系统往往不能满足工程建设的需要,所以必须针对不同的工程采用适合它的独立坐标系统。
线路独立坐标系的建立方法研究主要是研究线路工程中如何建立坐标系统而使其精度能满足工程需要。由于线路测量的特点是跨度较长,当采用国家统一坐标系时往往会因为离开中央子午线较远而使变形量超限,因此必须采用独立坐标系统。
由于线路工程的不同,因此需采用的独立坐标系统也不尽相同。所以针对不同的线路工程应采用不同的独立坐标系统。当线路工程是南北走向时由于线路基本上位于中央子午线上,因此不必要对多个独立坐标系统的转换衔接问题进行研究。当线路工程是东西走向时由于线路跨度较长而往往需要建立多个独立坐标系统,因此需要对多个独立坐标系统的转换衔接问题进行研究。
公路、铁路、架空送电线路以及输油管道等均属于线型工程,它们的中线统称线路。一条线路的勘测和设计工作,主要是根据国家的计划与自然地理条件,确定线路经济合理的位置。为达此目的,必须进行反复地实践和比较。
线路在勘测设计阶段首先要进行控制测量工作,由于在线路控制测量过程中,每条线路所在测区的位置不同且距离不可能很短,有的可能跨越一个投影带,二个投影带甚至更多,所以,在线路控制测量中,投影长度变形很容易超限,这就需要我们采取一定的措施来使投影长度变形减弱,将投影长度变形控制在允许的范围之内。最有效的方法就是建立与测区相适应的坐标系统。
坐标系统是所有测量工作的基础,所有测量成果都是建立在其上的,因此坐标系统选择的适当与否关系到整个工程的质量问题。对于线路工程而言,使投影长度变形控制在允许的精度范围之内是建立独立坐标系统主要解决的问题,因此,独立坐标系统的建立主要是根据线路的长度和所在测区的不同而建立与本测区和本线路相适应的坐标系统,从而使其投影长度变形控制在允许范围之内。
本文以线路控制测量为例,详细论述了线路独立坐标系统的建立方法。
2 高斯平面直角坐标系的建立
我们已经知道,大地坐标系是以椭球面为基准面的坐标系,它可以用来确定地面点在椭球面上的位置,但是如果用于大比例尺测图控制网以及工程控制网则不适应。因此通常是将椭球面上的元素,如大地坐标、长度、方向等转化至平面上,采用平面直角坐标系进行计算,本章就高斯平面直角坐标系的建立及相关问题进行了讨论。
2.1.1地球椭球的基本几何参数
参考椭球 具有一定的几何参数、定位及定向的用以代表某一地区大地水准面的地球椭球叫做参考椭球。地面上一切观测元素都应归算到参考椭球面上,并在该面上进行计算,它是大地测量计算的基准面,同时又是研究地球形状和地图投影的参考面。
有关元素如图1
O为椭球中心;
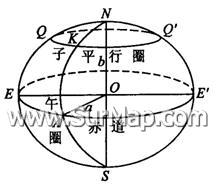
NS为旋转轴;
a为长半轴;
b为短半轴;
子午圈(或径圈或子午椭圆);
平行圈(或纬圈);
赤道。
旋转椭球的形状和大小是由子午椭圆的五个基本几何参数(元素) (图1:椭球参数示意图)
来决定的,即:
椭圆的长半轴: a
椭圆的短半轴: b
椭圆的扁率: ![]() (2-1)
(2-1)
椭圆的第一偏心率: 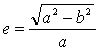 (2-2)
(2-2)
椭圆的第二偏心率: 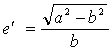 (2-3)
(2-3)
其中:a、b称为长度元素;
扁率![]() 反映了椭球体的扁平程度,如
反映了椭球体的扁平程度,如![]() =0时,椭球变为球体;
=0时,椭球变为球体;![]() =1时,则为平面。
=1时,则为平面。
e和e/是子午椭圆的焦点离开中心的距离与椭圆半径之比,它们也反映了椭球体的扁平程度,偏心率越大,椭球愈扁。
五个参数中,若知道其中的两个参数就可决定椭球的形状和大小,但其中至少应已知一个长度元素(如a或b),人们习惯于用![]() 和
和![]() 表示椭球的形状和大小,便于级数展开。引入下列符号:
表示椭球的形状和大小,便于级数展开。引入下列符号:
![]()
![]()
![]() (2-4)
(2-4)
式中B为大地纬度,c为极曲率半径(极点处的子午线曲率半径)。
两个常用的辅助函数,W第一基本纬度函数,V第二基本纬度函数。
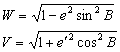 (2-5)
(2-5)
传统大地测量利用天文大地测量和重力测量资料推求地球椭球的几何参数,自1738年(法国)布格推算出第一个椭球参数以来,200多年间各国大地测量工作者根据某一国或某一地区的资料,求出了数目繁多,数值各异的椭球参数。由于卫星大地测量的发展,使推求总地球椭球体参数成为可能,自1970年以后的椭球参数都采用了卫星大地测量资料。长半经变化于6378135m~6378145m之间,扁率分母变化于298.25~298.26之间,可见精度已很高。比较著名的有30个椭球参数,其中涉及我国的如表1示:
(表1:椭球参数表)
|
椭球参数 |
年代 |
长半径m |
扁率分母 |
采用国家、地区 |
|
海福特 |
1906 |
6378283 |
297.8 |
美、阿根廷、比利时、大洋洲 |
|
克拉索夫斯基 |
1940 |
6378245 |
298.3 |
苏、东欧、中、朝鲜等 |
|
1975年大地坐标系 |
1975 |
6378140 |
298.257 |
1975年国际第三个推荐值 |
|
WGS-84 |
1984 |
6378137 |
298.25722 |
GPS定位系统 |
我国1954年北京坐标系应用的是克拉索夫斯基椭球参数,1980年西安坐标系应用的是1975年国际椭球参数,而GPS应用的是WGS-84系椭球参数。
2.1.2地球椭球参数间的相互关系
由(2-2)和(2-3)式得:
![]()
![]()
![]()
![]()
并得:
![]() (2-6)
(2-6)
推得: 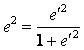
![]()
同理可得:
![]()
![]()
![]()
![]() (2-8)
(2-8)
![]() 。
。
2.2.1高斯投影与高斯平面直角坐标
地球投影 所谓地球投影,简略说来就是将椭球面各元素(包括坐标、方向和长度)按一定的数学法则投影到平面上。
![]() (2-9)
(2-9)
式中L,B是椭球面上某点的大地坐标,而![]() 是该点投影后的平面(投影面)直角坐标。
是该点投影后的平面(投影面)直角坐标。
式(2-9)表示了椭球面上一点同投影面上对应点之间坐标的解析关系,也叫做坐标投影公式。投影问题也就是建立椭球面元素与投影面相对应元素之间的解析关系式。投影的方法很多,如高斯投影、兰勃脱投影等。我国采用高斯投影。
高斯投影又称横轴椭圆柱等角投影,是德国测量学家高斯于1825~1830年首先提出的。实际上,直到1912年,由德国另一位测量学家克吕格推导出实用的坐标投影公式后,这种投影才得到推广,所以该投影又称高斯-克吕格投影。想象有一椭圆柱面横套
(图2:横轴椭圆柱等角投影示意图)
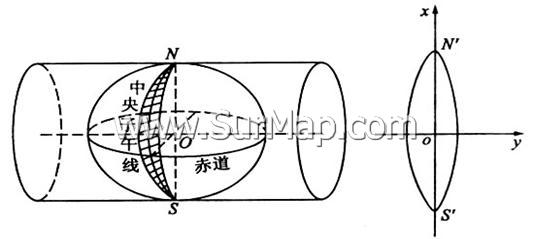
在地球椭球体外面,并与某一条子午线(称中央子午线或轴子午线)相切,椭圆柱的中心轴通过椭球体中心,然后用一定的投影方法将中央子午线两侧各一定经差范围内的地区投影到椭圆柱面上,再将此柱面展开即成为投影面。
我国规定按经差![]() 和
和![]() 度进行投影分带,大比例尺测图和工程测量一般采用
度进行投影分带,大比例尺测图和工程测量一般采用![]() 带投影。特殊情况下工程测量控制网也可用
带投影。特殊情况下工程测量控制网也可用![]() 带或任意带。
带或任意带。
高斯投影![]() 带自
带自![]() 子午线起每隔经差
子午线起每隔经差![]() 自西向东分带,依次编号1,2,3,…。我国
自西向东分带,依次编号1,2,3,…。我国![]() 带中央子午线的经度,由
带中央子午线的经度,由![]() 起每隔
起每隔![]() 而至
而至![]() ,共计12带,带号用n表示,中央子午线的经度用
,共计12带,带号用n表示,中央子午线的经度用![]() 表示,则
表示,则![]() 与n的关系为
与n的关系为![]() 。
。
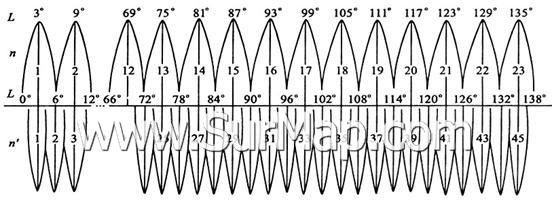
(图3:高斯投影分带示意图)
高斯投影![]() 带是自
带是自![]() 子午线每隔经差
子午线每隔经差![]() 自西向东分带,它的中央子午线一部分同
自西向东分带,它的中央子午线一部分同![]() 带中央子午线重合,一部分同
带中央子午线重合,一部分同![]() 带分界子午线重合,带号用n/表示,
带分界子午线重合,带号用n/表示,![]() 带中央子午线用L表示,关系是:
带中央子午线用L表示,关系是:![]() 。
。
在投影面上,中央子午线和赤道的投影都是直线,并且以中央子午线和赤道的交点O作为坐标原点,以中央子午线的投影为纵坐标轴,以赤道的投影为横坐标轴,这样便形成了高斯平面直角坐标系。在我国![]() 坐标均为正,
坐标均为正,![]() 坐标的最大值(在赤道上)约为330KM。为避免出现负的横坐标,可在横坐标上加500KM。此外还应在坐标前面冠以带号,这种坐标称为国家统一坐标。如某点Y=19123456.789m,该点位于19带内,其相对于中央子午线而言的横坐标是:首先去掉带号,再减去500KM,最后得y=-376543.211m。
坐标的最大值(在赤道上)约为330KM。为避免出现负的横坐标,可在横坐标上加500KM。此外还应在坐标前面冠以带号,这种坐标称为国家统一坐标。如某点Y=19123456.789m,该点位于19带内,其相对于中央子午线而言的横坐标是:首先去掉带号,再减去500KM,最后得y=-376543.211m。
由于分带造成了边界子午线两侧的控制点和地形图处于不同的投影带内,为了把各带连成整体,一般规定各投影带要有一定的重叠度,其中每一![]() 带向东加宽
带向东加宽![]() ,向西加宽
,向西加宽![]() ,这样在上述重叠范围内,控制点将有两套相邻带的坐标值,地形图将有两套公里格网,从而保证了边缘地区控制点间的互相应用,也保证了地图的拼接和使用。
,这样在上述重叠范围内,控制点将有两套相邻带的坐标值,地形图将有两套公里格网,从而保证了边缘地区控制点间的互相应用,也保证了地图的拼接和使用。
由于高斯投影是正形投影,故保证了投影的角度不变性、图形的相似性以及在某点各方向上长度比的同一性;由于采用了同样法则的分带投影,既限制了长度变形,又保证了在不同投影带中采用相同的简单公式和数表进行由于变形引起的各项改正的计算,且带与带间的互相换算也能用相同的公式和方法进行。高斯投影这些优点使它得到广泛的推广和具有国际性。
2.2.2高斯投影坐标正反算公式
2.2.2. 1高斯投影坐标正算公式: B,![]()
![]() x,y
x,y
高斯投影必须满足以下三个条件:
⑴中央子午线投影后为直线;⑵中央子午线投影后长度不变;⑶投影具有正形性质,即正形投影条件。
由第一条件知中央子午线东西两侧的投影必然对称于中央子午线,即![]() 式中,x为
式中,x为![]() 的偶函数,y为
的偶函数,y为![]() 的奇函数;
的奇函数;![]() ,即
,即![]() ,如展开为
,如展开为![]() 的级数,收敛。
的级数,收敛。
![]() (2-10)
(2-10)
式中![]() 是待定系数,它们都是纬度B的函数。
是待定系数,它们都是纬度B的函数。
由第三个条件知:
![]()
分别对![]() 和q求偏导数并代入上式
和q求偏导数并代入上式
 (2-11)
(2-11)
上两式两边相等,其必要充分条件是同次幂![]() 前的系数应相等,即
前的系数应相等,即
 (2-12)
(2-12)
(2-12)是一种递推公式,只要确定了![]() 就可依次确定其余各系数。
就可依次确定其余各系数。
由第二条件知:位于中央子午线上的点,投影后的纵坐标x应等于投影前从赤道量至该点的子午线弧长X,即(2-10)式第一式中,当![]() 时有:
时有:
![]() (2-13)
(2-13)
顾及(对于中央子午线)
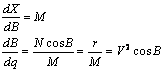
得:
![]() (2-14,15)
(2-14,15)
![]() (2-16)
(2-16)
依次求得![]() 并代入(2-10)式,得到高斯投影正算公式
并代入(2-10)式,得到高斯投影正算公式

 (2-17)
(2-17)
2.2.2. 2高斯投影坐标反算公式
x,y ![]() B,
B,![]()
投影方程:
![]() (2-18)
(2-18)
高斯投影坐标反算公式推导要复杂些。
⑴由x求底点纬度(垂足纬度)![]() ,对应的有底点处的等量纬度
,对应的有底点处的等量纬度![]() ,求x,y与
,求x,y与![]() 的关系式,仿照
的关系式,仿照![]() 式有,
式有,
![]()
由于y和椭球半径相比较小(1/16.37),可将![]() 展开为y的幂级数;又由于是对称投影,q必是y的偶函数,
展开为y的幂级数;又由于是对称投影,q必是y的偶函数,![]() 必是y的奇函数。
必是y的奇函数。
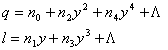 (2-19)
(2-19)
![]() 是待定系数,它们都是x的函数.
是待定系数,它们都是x的函数.
由第三条件知:
![]() ,
,
![]() , (2-20)
, (2-20)
(2-19)式分别对x和y求偏导数并代入上式
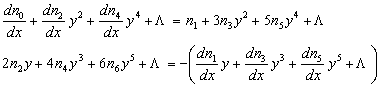 上式相等必要充分条件,是同次幂y前的系数相等,
上式相等必要充分条件,是同次幂y前的系数相等,
![]()
第二条件,当y=0时,点在中央子午线上,即x=X,对应的点称为底点,其纬度为底点纬度![]() ,也就是x=X时的子午线弧长所对应的纬度,设所对应的等量纬度为
,也就是x=X时的子午线弧长所对应的纬度,设所对应的等量纬度为![]() 。也就是在底点展开为y的幂级数。
。也就是在底点展开为y的幂级数。
由(2-19)1式
![]()
依次求得其它各系数
![]() (2-21)
(2-21)
![]() (2-21)1
(2-21)1
…………
将![]() 代入(2-19)1式得
代入(2-19)1式得

(2-22)1
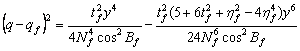
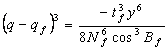 (2-22)
(2-22)
将![]() 代入(2-19)2式得(2-23)2式。(最后表达式)
代入(2-19)2式得(2-23)2式。(最后表达式)
⑵求![]() 与
与![]() 的关系。
的关系。
由式![]() 知:
知:
![]() (2-23)
(2-23)
![]() (2-24)
(2-24)
按台劳级数在![]() 展开
展开
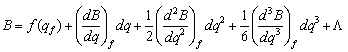 (2-25)
(2-25)
![]() (2-25)
(2-25)
由![]() 式可求出各阶导数:
式可求出各阶导数:
![]() (2-26)
(2-26)
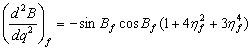 (2-27)1
(2-27)1
![]() (2-27)2
(2-27)2
…………………
将式(2-22)1(2-22)(2-26)(2-27)入(2-25)并按y幂集合得高斯投影坐标反算公式(2-28)
 (2-28)
(2-28)
归纳由![]() 求
求![]() 的基本思想:由点
的基本思想:由点![]() 得到底点
得到底点![]() ,将底点f作为过渡,也就是说将坐标原点o移到f点,先求
,将底点f作为过渡,也就是说将坐标原点o移到f点,先求![]() 关系式,再将
关系式,再将![]() 关系式代入
关系式代入![]() 关系式得
关系式得![]() 关系式,最后将坐标原点移回到o点,从而求得
关系式,最后将坐标原点移回到o点,从而求得![]() 点。
点。
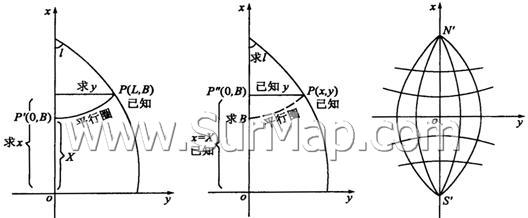
2.2.2. 3高斯投影坐标正反算公式的几何解释:
(图4:高斯投影坐标正反算公式的几何解释示意图)
⑴当B=0时x=X=0,y则随![]() 的变化而变化,这就是说,赤道投影
的变化而变化,这就是说,赤道投影
为一直线且为y轴。当![]() =0时,则y=0,x=X,这就是说,中央子午线投影亦为直线,且为x轴,其长度与中央子午线长度相等。两轴的交点为坐标原点。⑵当
=0时,则y=0,x=X,这就是说,中央子午线投影亦为直线,且为x轴,其长度与中央子午线长度相等。两轴的交点为坐标原点。⑵当![]() =常数时(经线),随着B值增加,x值增大,y值减小,这就告诉我们,经线是凹向中央子午线的曲线,且收敛于两极。又因
=常数时(经线),随着B值增加,x值增大,y值减小,这就告诉我们,经线是凹向中央子午线的曲线,且收敛于两极。又因![]() ,即当用-B代替B时,y值不变,而x值数值相等符号相反,这就说明赤道是投影的对称轴。⑶当B=常数时(纬线),随着的
,即当用-B代替B时,y值不变,而x值数值相等符号相反,这就说明赤道是投影的对称轴。⑶当B=常数时(纬线),随着的![]() 增加,x值和y值都增大,这就是说,纬线是凸向赤道的曲线。又当用-
增加,x值和y值都增大,这就是说,纬线是凸向赤道的曲线。又当用-![]() 代替
代替![]() 时,x值不变,而y值数值相等符号相反,这就说明,中央子午线是投影对称轴。由于满足正形投影条件,所以经线和纬线的投影是互相垂直的。⑷距中央子午线愈远的子午线,投影后弯曲愈厉害,表明长度变形愈大。
时,x值不变,而y值数值相等符号相反,这就说明,中央子午线是投影对称轴。由于满足正形投影条件,所以经线和纬线的投影是互相垂直的。⑷距中央子午线愈远的子午线,投影后弯曲愈厉害,表明长度变形愈大。
2.2.3坐标的换带计算
为了限制高斯投影长度变形,将椭球面按一定经度的子午线划分成不同的投影带;或者为了抵偿长度变形,选择某一经度的子午线作为测区的中央子午线。由于中央子午线的经度不同,使得椭球面上统一的大地坐标系,变成了各自独立的平面直角坐标系,就需要将一个投影带的平面直角坐标系,换算成另外一个投影带的平面直角坐标,称为坐标换带。
2.2.3. 1坐标换带的方法
坐标换带有直接换带计算法和间接换带计算法两种。目前采用间接换带计算法,因此下面仅就此方法作一介绍。
如将第一带(东带或西带)的平面坐标换算为第二带(西带或东带)的平面坐标,方法是先根据第一带的平面坐标x,y和中央子午线的经度L。按高斯投影坐标反算公式求得大地坐标B,L然后根据B,L和第二带的中央子午线经度![]() 按高斯投影坐标正算公式求得在第二带中的平面坐标
按高斯投影坐标正算公式求得在第二带中的平面坐标 ![]() ,
,![]() 。由于在换带计算中,把椭球面上的大地坐标作为过渡坐标,因而称为间接换带法。这种方法理论上是严密的,精度高,而且通用性强,他适用于6°带与6°带,3°带与3°带,6°带与3°带之间的坐标换带。虽然这种方法计算量较大,但可用电子计算机计算来克服,故已成为坐标换带中最基本的方法。
。由于在换带计算中,把椭球面上的大地坐标作为过渡坐标,因而称为间接换带法。这种方法理论上是严密的,精度高,而且通用性强,他适用于6°带与6°带,3°带与3°带,6°带与3°带之间的坐标换带。虽然这种方法计算量较大,但可用电子计算机计算来克服,故已成为坐标换带中最基本的方法。
2.2.3. 2坐标换带的实际应用
在生产实践中通常有以下两种情况需要换带计算
⑴控制网中的已知点位于相邻的两个投影带中。如图5
(图5:坐标换带示意图)
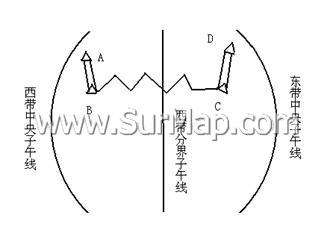 中的附合导线,A,B,C,D为已知高级点。A,B 两点位于西带内,具有西带的高斯平面直角坐标值;C,D两点位于东带内,具有东带的高斯平面直角坐标值。在坐标平差计算时,就必须将它们的坐标系统统一起来,或是将A,B点的西带坐标值换算至东带,或是将C,D点的东带坐标值换算至西带。
中的附合导线,A,B,C,D为已知高级点。A,B 两点位于西带内,具有西带的高斯平面直角坐标值;C,D两点位于东带内,具有东带的高斯平面直角坐标值。在坐标平差计算时,就必须将它们的坐标系统统一起来,或是将A,B点的西带坐标值换算至东带,或是将C,D点的东带坐标值换算至西带。
⑵国家控制点的坐标通常是6°带的坐标,而在工程测量中往往需要采用![]() 带或1.5°带,这就产生了6°带与
带或1.5°带,这就产生了6°带与![]() 带或 1.5°带之间的坐标换算问题。
带或 1.5°带之间的坐标换算问题。
我们知道,![]() 带的中央子午线中,有半数与6°带的中央子午线重合。所以,由6°带到3°带的换算区分为2种情况:
带的中央子午线中,有半数与6°带的中央子午线重合。所以,由6°带到3°带的换算区分为2种情况:
① 3°带与6°带的中央子午线重合 如图所示,3°带第
(图6:坐标换带示意图)
41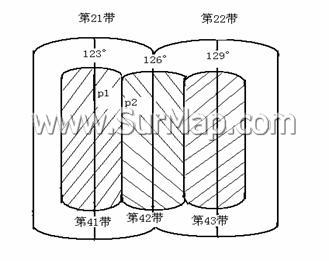
带与6°第21带的中央子午线重合。既然中央子午线一致,坐标系统也就一致。所以,图中P1点在6°带第21带的坐标,也就是该点在3°带第41带的坐标。在这种情况下,6°带与3°带之间,不存在换带计算问题。
② 3°带中央子午线与6°带分带子午线不重合如图所示,若已知P2点在6°带第21带的坐标,求它在3°带第42带的坐标。由于这2个投影带的中央子午线不同,坐标系统不一致,必须进行换带计算。不过P2点在6°带第21带的坐标与它在3°第41带的坐标相同,所以6°带到3°带坐标换算,也可看作是3°带到3°带的邻带坐标换算。
换带计算目前广泛采用高斯投影坐标正反算方法 ,他适用于任何情况下的换带计算工作。这种方法的程序是:首先将某投影带的已知平面坐标(x1,y1 ),按高斯投影坐标反算公式求得其大地坐标(B,L);然后根据纬度B和对于所选定的中央子午线的经差![]() ,按高斯投影坐标正算公式求其在选定的投影带的平面坐标(x2,y2)。
,按高斯投影坐标正算公式求其在选定的投影带的平面坐标(x2,y2)。
例如,某点A在新54坐标系6°带的平面坐标为
x1=3589644.287
y1=20679136.439
求A点在3°带的平面直角坐标(x2,y2).
首先确定A点所在投影带中央子午线经度。由横坐标的规定值可以直接判定,A点位于6°带第20带,其中央子午线经度L。=117°,横坐标的自然值为y1=679136.493-500000=+179136.439m;该坐标等同于3°带第39带的平面坐标。
其次将已知的6°带坐标反算为大地坐标。为此,可直接应用坐标反算公式进行计算,其结果为
B=32°24![]() 57.6522"
57.6522"
L=118°54![]() 15.2206"
15.2206"
由大地经度L可判断,A点位于3°第40带,中央子午线为L。=120°。
最后根据高斯投影坐标正算公式,由已知的纬度B和经度![]() 计算A点在3°带第40带的平面直角坐标,得
计算A点在3°带第40带的平面直角坐标,得
x2=3588576.591
y2=40396922.874
其中横坐标y2为规定值。
2.2.3. 3相邻带坐标换算存在的问题及解决方案
在具有不同抵偿高程面的两个相邻投影带之间进行坐标换带计算时,由于具有不同的抵偿高程面而使一个带中的坐标换至相邻带时使长度变形超线,在线路工程测量中就需要进行精度预算,从而在进行坐标换带计算时使长度变形控制在允许的范围内。其基本方法如下:
根据高斯投影长度综合变形公式![]() 将长度综合变形容许值1:40000代入上式即可得到下列方程
将长度综合变形容许值1:40000代入上式即可得到下列方程![]() 对于已知高程面的测区,利用该式可以计算出相对变形不超过1:40000的投影带内y坐标的取值范围,根据y坐标的取值范围使在布设控制导线边时,使跨带边的长度变形在y坐标的取值范围之内,这样就可以进行换带计算而不使综合长度变形超线。其具体解决方案如下:
对于已知高程面的测区,利用该式可以计算出相对变形不超过1:40000的投影带内y坐标的取值范围,根据y坐标的取值范围使在布设控制导线边时,使跨带边的长度变形在y坐标的取值范围之内,这样就可以进行换带计算而不使综合长度变形超线。其具体解决方案如下:
⑴国家统一![]() 带相邻带的坐标换算方法:
带相邻带的坐标换算方法:
在线路工程中,如果由于线路过长而需要进行相邻带的坐标换算,这是就需要对控制点进行精度预算,从而使换带计算顺利进行。其主要方法如图:
根据高斯投影长度综合变形公式![]() 将长度综合变形容许
将长度综合变形容许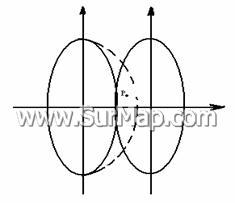
(图7:坐标换带示意图)
值1:40000代入上式即可得到下列方程![]() 对于已知高程面的测区,利用该式可以计算出相对变形不超过1:40000的投影带内y坐标的取值范围,根据y坐标的取值范围使在布设控制导线边时使P点处于41带的扩展区域内,该扩展区内所有的点都满足精度要求。这样P点在两个投影带中都满足精度要求同时又利于换带计算。利用这种方法就可以很方便的进行相邻带的坐标换算。
对于已知高程面的测区,利用该式可以计算出相对变形不超过1:40000的投影带内y坐标的取值范围,根据y坐标的取值范围使在布设控制导线边时使P点处于41带的扩展区域内,该扩展区内所有的点都满足精度要求。这样P点在两个投影带中都满足精度要求同时又利于换带计算。利用这种方法就可以很方便的进行相邻带的坐标换算。
⑵![]() 带相邻带的换带计算
带相邻带的换带计算
当国家统一![]() 带不能满足精度要求时,即如上图P点在相交处不能达到精度要求时就必须考虑其他方法来解决此问题。
带不能满足精度要求时,即如上图P点在相交处不能达到精度要求时就必须考虑其他方法来解决此问题。
由于投影带划分的目的是限制高斯投影长度变形,所以可以通过细分投影带的方法来限制高斯投影长度变形。
其方法是:如图P点,当该点在![]() 带第42带换算至第41带时不能满足精度要求时,就可以通过在原
带第42带换算至第41带时不能满足精度要求时,就可以通过在原![]() 带的基础上细划分为
带的基础上细划分为![]() 带从而减少高斯投影长度变形,这样相邻带之间在满足精度要求的基础上就有
带从而减少高斯投影长度变形,这样相邻带之间在满足精度要求的基础上就有
(图8:坐标换带示意图)
一部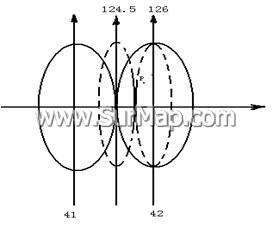 分扩展区域,在这部分扩展区域内所有的点在相邻带都满足精度要求,这样就可以用如上1分析的方法进行相邻带之间的坐标换算。
分扩展区域,在这部分扩展区域内所有的点在相邻带都满足精度要求,这样就可以用如上1分析的方法进行相邻带之间的坐标换算。
3 独立坐标系统的建立
在工程建设地区(如公路、铁路、管线)布设测量控制网时,其成果不仅要满足1:500比例尺测图需要,而且还应满足一般工程放样的需要。在线路测量中,总是要将测得的数据经计算再放到实地而施工放样时要求控制网由坐标反算的长度与实测的长度尽可能相符,但国家坐标系的成果很难满足这样的要求,这是因为国家坐标系每个投影带(高斯投影)都是按一定的间隔(6°或3°)划分,由西向东有规律地分布.由于每项工程的建设地区不同,且国家坐标系统的高程归化面是参考椭球面,各地区的地面位置与参考椭球面都有一定的距离,这两项将产生高斯投影变形改正和高程归化改正,经过这两项改正后的长度不可能与实测的长度相等。
建立独立坐标系的主要目的就是为了减小高程归化与投影变形产生的影响,因此必须将它们控制在一个微小的范围内,使计算出来的长度在实际利用时(如工程放样)不需要做任何改算。
本章就如何建立独立坐标系统而使其长度变形控制在允许范围内作详细讨论。
3.1.1测量投影面与投影带的选择
3.1.1. 1 有关投影变形的基本概念
平面控制测量投影面和投影带的选择,主要是解决长度变形问题。这种投影变形主要由以下两方面因素引起:
⑴实量边长归算到参考椭球体面上的变形影响 ![]() (3-1)
(3-1)
其推导过程为: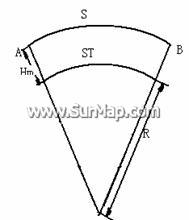
(图9:实量边长归算到参考椭球体面示意图)
由图知![]()
由上式可得![]() 从而可得
从而可得
![]()
式中,![]() 为归算边高出参考椭球面的平均高程;
为归算边高出参考椭球面的平均高程;
S为归算边的长度 ;
![]() 为实量边长在参考椭球面上的长度
为实量边长在参考椭球面上的长度
R为归算边方向参考椭球法截弧的曲率半径。
归算边的相对变形为:
![]() (3-2)
(3-2)
由公式可以看出: ![]() 值与
值与![]() 成正比,随
成正比,随![]() 增大而增大。
增大而增大。
⑵将参考椭球面上边长归算到高斯投影面上的变形影响
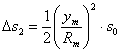 (3-3)
(3-3)
式中,![]() ,即
,即![]() 为投影归算边长即
为投影归算边长即![]() ,
,
![]() 为归算边两端点横坐标平均值,
为归算边两端点横坐标平均值,
![]() 为参考椭球面平均曲率半径。
为参考椭球面平均曲率半径。
投影边的相对变形为:
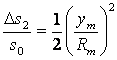 (3-4)
(3-4)
由公式可以看出:![]() 的值总为正,即椭球面上长度归算至高斯面上,总是增大的,
的值总为正,即椭球面上长度归算至高斯面上,总是增大的,![]() 值与
值与![]() 成正比而增大,离中央子午线愈远变形愈大。
成正比而增大,离中央子午线愈远变形愈大。
3.1.1. 2 有关工程测量平面控制网的精度要求的概念
为便于施工放样的顺利进行,要求由控制点坐标直接反算的边长与实地量得的边长,在长度上应该相等,即由上述两项归算投影改正而带来的变形或改正数,不得大于施工放样的精度要求。一般地,施工放样的方格网和建筑轴线的测量精度为1/5000~1/20000。因此,由归算引起的控制网长度变形应小于施工放样允许误差的1/2,即相对误差为1/10000~1/40000,也就是说,每公里的长度改正数,不应该大于10~2.5cm。
3.1.1. 3工程测量投影面和投影带选择的基本出发点
⑴ 在满足精度要求的前提下,为使测量结果一测多用,应采用国家统一![]() 带高斯平面直角坐标系,将观测结果归算至参考椭球面上。即工程测量控制网应同国家测量系统相联系;
带高斯平面直角坐标系,将观测结果归算至参考椭球面上。即工程测量控制网应同国家测量系统相联系;
⑵当边长的两次归算投影改正不能满足上述要求时,为保证测量结果的直接利用和计算的方便,可采用任意带的独立高斯平面直角坐标系,归算测量结果的参考面可自己选定。为此可用以下手段实现:① 通过改变![]() 从而选择合适的高程参考面,将抵偿分带投影变形(称为抵偿投影面的高斯正形投影);② 改变
从而选择合适的高程参考面,将抵偿分带投影变形(称为抵偿投影面的高斯正形投影);② 改变![]() 从而对中央子午线作适当移动,以抵偿由高程面的边长归算到参考椭球面上的投影变形(称为任意带高斯正形投影);③ 通过既改变
从而对中央子午线作适当移动,以抵偿由高程面的边长归算到参考椭球面上的投影变形(称为任意带高斯正形投影);③ 通过既改变![]() (选择高程参考面),又改变
(选择高程参考面),又改变![]() (移动中央子午线),来抵偿两项归算改正变形(称为具有高程抵偿面的任意带高斯正形投影)。
(移动中央子午线),来抵偿两项归算改正变形(称为具有高程抵偿面的任意带高斯正形投影)。
3.1.2 投影改正值的变化规律
一般情况下,将投影改正作为常数看待,不考虑测区内不同位置投影改正值的变化问题。然而在实际情况中,即使在地形比较平坦的地区或较小范围的测区,其影响也是不容忽视的。
设测区中任一点 k 与测区中心在东西方向(y轴)上的距离为y,与测区平均高程的高差为h 。k点的两项投影改正与测区中心过平均高程面的改正是不一样的。
3.1.2. 1观测值化至参考椭球面投影改正值的变化
k 点的大地水准面投影改正为:
![]()
上式中等号右边的第二项即为椭球面投影改正的变化量,令
![]()
![]()
由上式可知,高差h与投影改正的变化量![]() 成正比,
成正比,![]() 随着h的增大而增大。
随着h的增大而增大。
3.1.2. 2椭球面上的观测值化至高斯平面投影改正值的变化
k点的高斯平面投影改正为:
![]()
令 ![]()
![]()
上式即为椭球面上的观测值化至高斯平面投影改正的变化量。
由上式可见,若s为常量![]() 与y 和
与y 和![]() 两个变量有关,其规律为:
两个变量有关,其规律为:
⑴当![]() =0时,中央子午线在测区中心。
=0时,中央子午线在测区中心。
⑵![]() 与
与![]() 成正比关系,
成正比关系,![]() 随着
随着![]() 值的增加而增加;
值的增加而增加;
⑶![]() 与y 成抛物线的关系,
与y 成抛物线的关系,![]() 随着y的增加而增加;
随着y的增加而增加;
⑷当![]() 一定时,随着
一定时,随着![]() (y)的值增加,y(
(y)的值增加,y(![]() )的值急剧减小。
)的值急剧减小。
3.1.3观测值化至椭球面上的计算
3.1.3. 1预备计算
其内容包括水平方向的归化改正(三差改正)、长度归化改正和天文方位角归化为大地方位角的计算。在这些公式中需要有关边长的近似大地方位角,为此需进行一些必要的预备计算工作。
⑴ 三角形闭合差及测角中误差的计算
计算三角形闭合差的目的是为了计算近似平面归化角和测角中误差;而求近似平面归化角的目的是为求近似坐标方位角和各点的近似坐标做准备。
三角形闭合差按下式计算:
![]() (3-5)
(3-5)
测角中误差按菲列罗公式计算
![]() (3-6)
(3-6)
式中w为三角形闭合差(按2-33式计算),n为三角形个数。
⑵ 近似坐标计算
为计算近似子午线收敛角(为求近似大地方位角用)及方向改化和距离改正,需计算各三角点的近似坐标。坐标的计算有两种方法:
变形戎格公式:
![]()
![]() (3-7)
(3-7)
坐标增量公式:
![]()
![]() (3-8)
(3-8)
当有两个已知点坐标时,前式计算较为方便,否则用后式为好。式中![]() 为近似平面边长,由近似边长计算得到。
为近似平面边长,由近似边长计算得到。![]() 为近似坐标方位角,由已知的坐标方位角和近似平面角推算得到。近似坐标计算到0.1m(若三四等计算至1m)。高等级控制网要求归化工作很高精度时,有时需经过二次趋近计算近似坐标才能满足要求(三四等一般只计算一次即可)。
为近似坐标方位角,由已知的坐标方位角和近似平面角推算得到。近似坐标计算到0.1m(若三四等计算至1m)。高等级控制网要求归化工作很高精度时,有时需经过二次趋近计算近似坐标才能满足要求(三四等一般只计算一次即可)。
⑶ 近似子午线收敛角及近似大地方位角的计算
计算目的是为了计算近似大地方位角,而计算近似大地方位角的目的是为满足观测值归化至椭球面上的各项计算所需。
近似子午线收敛角公式: ![]() (3-9)
(3-9)
式中 ![]() ,
, ![]()
K和![]() 可在《测量计算用表》中以近似坐标x,y查取。
可在《测量计算用表》中以近似坐标x,y查取。
近似大地方位角的计算公式: ![]() (3-10)
(3-10)
式中![]() 抄自近似坐标计算时的近似坐标方位角。
抄自近似坐标计算时的近似坐标方位角。
⑷已知数据的换算
平面直角坐标换算为大地坐标
为计算已知点的子午线收敛角![]() 和垂线偏差分量,当已知点的起算坐标为高斯投影平面直角坐标x,y时,则应将其换算为大地坐标。公式即为高斯投影坐标反算公式(计算过程与前面介绍的完全相同)
和垂线偏差分量,当已知点的起算坐标为高斯投影平面直角坐标x,y时,则应将其换算为大地坐标。公式即为高斯投影坐标反算公式(计算过程与前面介绍的完全相同)
![]()
![]() (3-11)
(3-11)
⑸ 垂线偏差分量的计算
为对水平方向施加垂线偏差改正,必须计算各点的垂线偏差分量![]() 。若有测区范围的垂线偏差图,则可根据各三角点的近似坐标查取,而不必进行该项计算。如无分量图,应视情况采用不同方法进行计算。
。若有测区范围的垂线偏差图,则可根据各三角点的近似坐标查取,而不必进行该项计算。如无分量图,应视情况采用不同方法进行计算。
对有天文观测资料(天文经纬度)的全部三角点,按下式计算:
![]() (3-12)
(3-12)
对有重力资料的三角点按下式计算:
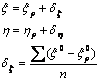 (3-13)
(3-13)
![]()
将算得的垂线![]() 线分别标在图上,并据其数值内插描绘
线分别标在图上,并据其数值内插描绘![]() 的等间隔曲线,则其余控制点的
的等间隔曲线,则其余控制点的![]() 值可在该图上内插得到。将获得的
值可在该图上内插得到。将获得的![]() 取至
取至![]() (对于三、四等三角测量,在我国东部平原地区,当
(对于三、四等三角测量,在我国东部平原地区,当![]() 时,可不进行此项计算。)
时,可不进行此项计算。)
⑹大地水准面差距的计算
为将基线长度归算至参考椭球面以及为了在水平方向中加入标高差改正数,需计算各点的大地水准面差距![]() 。如有大地水准面差距图,可采用天文水准的方法推求,其公式为:
。如有大地水准面差距图,可采用天文水准的方法推求,其公式为:
![]() (3-14)
(3-14)
大地水准面差距![]() 也可由大地水准面差距图中查取的。有时在平原地区由于
也可由大地水准面差距图中查取的。有时在平原地区由于![]() 不大,往往略去该项计算。
不大,往往略去该项计算。
⑺ 三角点上的三角高程计算
为了计算三差改正中的“标高差”改正数,必须要知道各三角点的高程。在没有几何水准测定高程的三角点上,可用三角高程方法推求,其公式为:
![]() (3-15)
(3-15)
式中![]() 为已知点高程,S为两点间球面边长,
为已知点高程,S为两点间球面边长, ![]() 为观测的高度角,c为地球曲率半径和大气折光差改正数,
为观测的高度角,c为地球曲率半径和大气折光差改正数,![]() 及
及![]() 分别为测站点仪器高和照准点标高,
分别为测站点仪器高和照准点标高,![]() 为高差改正项,
为高差改正项,![]() 或
或![]() ,当两点高差小于1000m时,可略去
,当两点高差小于1000m时,可略去![]() 的计算。
的计算。
3.1.3. 2观测值化至椭球面上的计算
⑴观测方向值归化改正数的计算
水平方向归化到椭球面上须在测站平差和归心改正后的方向值中加入以下三项改正:
① 垂线偏差改正
计算公式为
![]() (3-16)
(3-16)
计算取至![]() (三、四等三角测量通常不计算
(三、四等三角测量通常不计算![]() ,只有当
,只有当![]() 时才考虑
时才考虑![]() 的改正,此时取至
的改正,此时取至![]() 即可)。
即可)。
② 标高差改正
计算公式为:
![]() (3-17)
(3-17)
式中![]() 为照准点的海拔高程,
为照准点的海拔高程,![]() 为照准点的大地水准面差距,
为照准点的大地水准面差距,![]() 为标高。
为标高。![]() 按
按![]() 在《测量计算用表》中查取。
在《测量计算用表》中查取。![]() 算至
算至![]() (三、四等测量时,通常不考虑
(三、四等测量时,通常不考虑![]() ,但当
,但当![]() 时,应计算
时,应计算![]() 改正,计算取至
改正,计算取至![]() 即可)。
即可)。
③ 由法截弧方向化为大地线方向的改正
计算公式为:
![]() (3-18)
(3-18)
式中![]() 按S和B在《测量计算用表》中查取。因
按S和B在《测量计算用表》中查取。因![]() 很小,只有在一等三角测量概算时才计算。
很小,只有在一等三角测量概算时才计算。
三项改正计算后,并取各改正数的代数和,然后化算为归零值,即得到观测方向值归化至椭球面上的改正数。把归算至标石中心的观测方向值加上相应的归化改正数,便获得归化到椭球面上的方向值。
⑵ 基线长度和观测边长的归化改正
起算边长及实测边长都应归化为椭球面上的大地线长度。归化公式为 ![]() (3-19)
(3-19)
式中![]() 为边长归化改正数,d为经倾斜及归心改正后的实测边长,s为椭球面上相应的大地线长度,
为边长归化改正数,d为经倾斜及归心改正后的实测边长,s为椭球面上相应的大地线长度,![]() 为归化边长高出椭球面的平均高程(大地高),R为归化边长方向法截弧曲率半径。
为归化边长高出椭球面的平均高程(大地高),R为归化边长方向法截弧曲率半径。
⑶起始方位角的化算
已知的起始天文方位角或实测的天文方位角都必须归化成椭球面上大地方位角。其计算公式为:
![]() (3-20)
(3-20)
式中![]() 为观测的天文方位角,
为观测的天文方位角,![]() 分别为测站点的天文经、纬度,
分别为测站点的天文经、纬度,![]() 为测站点的大地经度,
为测站点的大地经度,![]() 为垂线偏差改正。
为垂线偏差改正。
至此,已将地面观测值都归化到椭球面。
3.1.4椭球面上的观测值化至高斯平面上的计算
为了在平面上进行平差,还必须将椭球面上的观测值化至高斯平面上,这项工作包括方向改化、距离改化和大地方位角化算为坐标方位角等三项内容。
3.1.4. 1方向改化的计算
为将椭球面上方向值化算到高斯平面上,需计算方向改化用的方向改正数。公式为:
![]()
![]() (3-21)
(3-21)
三、四等方向改正计算公式
![]() (3-22)
(3-22)
以上两式![]() ,《由高斯克吕格计算用表》按两点间平均纬度
,《由高斯克吕格计算用表》按两点间平均纬度![]() 查取。x,y均抄自近似坐标计算,取至0.1m。方向改化为每个三角形三个内角的角度方向改化之代数和应等于该三角形的球面角超的反号,以此作为方向改正数计算正确性的检核,不符值应在
查取。x,y均抄自近似坐标计算,取至0.1m。方向改化为每个三角形三个内角的角度方向改化之代数和应等于该三角形的球面角超的反号,以此作为方向改正数计算正确性的检核,不符值应在![]() 内(三、四等应在
内(三、四等应在![]() 之内)。归零后再加到已归化至椭球面上的方向值上,于是便得到化算至高斯平面上的方向值(取至
之内)。归零后再加到已归化至椭球面上的方向值上,于是便得到化算至高斯平面上的方向值(取至![]() ,三、四等取至
,三、四等取至![]() )。
)。
3.1.4. 2距离改化计算
为把椭球面上大地线的长度化算为高斯平面上的直线长度,需计算距离改化的改正数,其公式为:
![]() (3-23)
(3-23)
其中S为椭球面上大地线长度,D为高斯平面上长度。![]() ,以km为单位,
,以km为单位,![]() 抄自近似坐标计算。
抄自近似坐标计算。![]() 以
以![]() 为引数从《测量计算用表》中查取,以km为单位,距离改化计算值取至1mm。
为引数从《测量计算用表》中查取,以km为单位,距离改化计算值取至1mm。
3.1.4. 3大地方位角化算为坐标方位角的计算
为在高斯平面上进行坐标计算,要求推求各边的坐标方位角,为此需把起始大地方位角化算成坐标方位角,计算公式为:
![]()
式中![]() 为大地方位角,
为大地方位角,![]() 为起算点的子午线收敛角,可由起算点的坐标算得,
为起算点的子午线收敛角,可由起算点的坐标算得,![]() 为起始方向的方向改化值。
为起始方向的方向改化值。
至此,观测成果及有关已知数据的化算工作已全部结束。
3.2.1抵偿投影面的 带高斯正形投影平面直角坐标系
带高斯正形投影平面直角坐标系
这种坐标系仍采用国家![]() 带高斯正形投影,但投影的高程面不用参考椭球面而另选用一高程参考面,借以补偿因高斯投影带来的长度变形。在这个高程参考面上,投影长度变形为零。
带高斯正形投影,但投影的高程面不用参考椭球面而另选用一高程参考面,借以补偿因高斯投影带来的长度变形。在这个高程参考面上,投影长度变形为零。
公式(3—1)表明,将距离由较高的高程面化算至较低的椭球面时,长度总是减小的;公式(3—3)表明,将椭球面上的距离化算至高斯平面时,长度总是增加的。所以两个投影过程对长度变形具有抵偿的性质。如果恰当选择椭球的半径,使距离化算到这个椭球面上所减小的数值,恰好等于由这个椭球面化算至高斯平面所增加的数值的话,那么,高斯平面上的距离就同实地的距离一致了。这个适当的椭球面,就称之为“抵偿高程面”。
欲使长度综合变形得以抵偿,最好是以测区中心的综合长度变形为0 ,既δ= 0 ,也就是保证 : ![]() 。
。
将推导公式![]() 所引用的关系和数据代入,则有
所引用的关系和数据代入,则有
![]()
式中,若y以百公里为单位,H以米作为单位,则有
H = 785![]() (3-24)
(3-24)
利用上式就可以确定抵偿高程面的位置。例如,某地中心在高斯投影带的坐标为 y =91 km ,该地区的平均高程为400 m ,按上式算得:
H = 785 ![]()
![]() =650 m
=650 m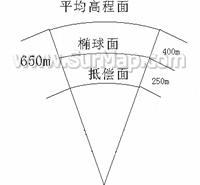
(图10:以抵偿面作投影面示意图)
即抵偿面应比高程面低650 m 如图所示:
抵偿面的高程应为![]()
抵偿面的位置确定后,就可以选择其中一个国家控制点作为“原点” ,保持它在国家![]() 带内的国家统一坐标值(
带内的国家统一坐标值(![]() ,
,![]() )不变,而将其他大地控制点的坐标(X ,Y)换算到抵偿高程面相对应的坐标系中去,换算公式为:
)不变,而将其他大地控制点的坐标(X ,Y)换算到抵偿高程面相对应的坐标系中去,换算公式为:
![]()
![]()
![]()
式中,R为该地区平均纬度处的椭球平均曲率半径。这样,经过上式换算的大地控制点坐标就可以作为控制测量的起算数据。
通过上述方法测得的控制点的局部坐标系中的坐标,可以按下式反算成国家统一坐标系内的坐标:
![]()
![]()
![]()
![]()
可以看出,通过此方法建立的独立坐标系,其测区中心的综合变形为 0 ,但离测区中心越远,变形也就越大,抵偿面与平均高程面的高差越大,测区的范围越小,而由(3—24)可知,此高差是由测区中心距![]() 带中央子午线的距离来决定的,也就是说,测区中心离中央子午线越远,测区的范围也就越小,这些可以由变形相似公式推导出来:
带中央子午线的距离来决定的,也就是说,测区中心离中央子午线越远,测区的范围也就越小,这些可以由变形相似公式推导出来:
![]()
而在实际应用中![]() 的允许值大都为2.5 cm/km,即1:4万,将其代入上式,即得:
的允许值大都为2.5 cm/km,即1:4万,将其代入上式,即得:
![]()
![]()
此式中,y的单位为km,H的单位也是 km,将此式改变一下,并保持y的单位不变,H以米作为单位,则得到:
当H < 170 m时 ![]()
当H >170m时 ![]()
![]()
![]()
将此式标注为(3—25)
由(3—24)式可以由测区中心算出抵偿高程面的位置,而由(3—25)式可以由抵偿高程面的高低计算测区的范围。因此,测区中心的位置![]() 决定了高程抵偿面的位置和测区范围。
决定了高程抵偿面的位置和测区范围。
为了更加明了的,并方便实际应用,可以计算得出下表:
(表2: 以测区中心决定的抵偿面位置及测区范围)
|
测区中心距中央子午线的位置 |
抵偿高程面的位 置H (km) |
测区范围(km) |
|
0 |
0 |
- 45 ~ 45 |
|
20 |
31.4 |
- 29 ~ 49 |
|
40 |
126 |
- 20 ~ 60 |
|
50 |
196 |
21 ~ 67 |
|
60 |
283 |
39 ~ 75 |
|
80 |
502 |
66 ~ 92 |
|
100 |
785 |
89 ~ 110 |
|
120 |
1130 |
111 ~ 128 |
3.2.2任意带高斯正形投影平面直角坐标系
这种坐标系仍将地面观测结果归算至参考椭球面上,但不采用国家![]() 带统一的分带方法而选择测区中心子午线作为中央子午线,借以补偿因实测结果算至参考椭球面带来的长度变形。
带统一的分带方法而选择测区中心子午线作为中央子午线,借以补偿因实测结果算至参考椭球面带来的长度变形。
不同投影带的出现,是因为选择了不同经度的中央子午线的缘故。如果合适的选择中央子午线的位置,使长度投影到该带所产生的变形,恰好抵偿这一长度投影到椭球面所产生的变形,此时,高斯投影面上的长度仍然和实地的长度一致。我们称这种抵偿长度变形的投影带为“任意投影带” 。
根据综合变形长度相对变形形式
![]()
可知,测区中心离子午线的距离 y 的选择与允许相对误差和测区的平均高程有关。
将长度综合变形的允许值1:4万代入上式,即可得:
![]() = 0.78
= 0.78![]() ·
·![]()
![]() (3—26)
(3—26)
对于某已知高程面的测区,利用上式可以计算出相对的变形不超过1:4万的国家统一![]() 带内的 y 坐标取值范围;同理,对于
带内的 y 坐标取值范围;同理,对于![]() 带内的不同投影区域,可以算出综合变形不超过允许数值时测区的平均高程的取值范围。
带内的不同投影区域,可以算出综合变形不超过允许数值时测区的平均高程的取值范围。
如果测区中心的![]() 坐标为横轴,取测区的平均高程H为纵轴,根据式(3—26)就可以画出相对变形恒为允许数值之间的两条曲线。这两条曲线就是适用于控制测量的投影带范围的临界限,或者说两条曲线间的区域就是适用于城镇测图和工程测量的投影带范围。
坐标为横轴,取测区的平均高程H为纵轴,根据式(3—26)就可以画出相对变形恒为允许数值之间的两条曲线。这两条曲线就是适用于控制测量的投影带范围的临界限,或者说两条曲线间的区域就是适用于城镇测图和工程测量的投影带范围。
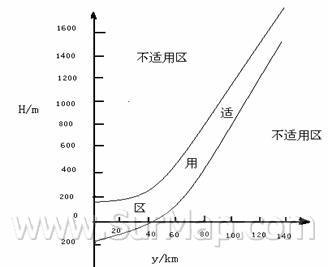
(图11:测区适用范围示意图)
如果根据式(3—26)画图,可以直观形象的判断国家统一![]() 带坐标系是否适合于本测区的需要。如果根据本测区的平均高程和
带坐标系是否适合于本测区的需要。如果根据本测区的平均高程和![]() 带 y坐标所确定的位置,处于两曲线以外的“不适用区” ,就应该考虑另行选择坐标系。
带 y坐标所确定的位置,处于两曲线以外的“不适用区” ,就应该考虑另行选择坐标系。
由公式(3—25)
当H < 170 m时 ![]()
当H >170m时 ![]()
![]()
![]()
可以根据测区平均高程计算由此方法可以适用的范围。为方便应用,可以计算编制下表:
(表3:以测区平均高程确定的任意带子午线位置及测区范围)
|
测区平均高程H(m) |
中央子午线离测区中心位置(km) |
测区的范围(km) |
|
0 |
0 |
-45~45 |
|
100 |
36 |
-21~57 |
|
150 |
44 |
-19~63 |
|
200 |
50 |
21~67 |
|
300 |
62 |
42~76 |
|
400 |
71 |
55~84 |
|
500 |
80 |
65~92 |
|
600 |
87 |
74~98 |
|
700 |
94 |
82~105 |
|
800 |
101 |
90~110 |
|
900 |
107 |
97~116 |
|
1000 |
113 |
103~121 |
|
1100 |
118 |
109~126 |
|
1200 |
124 |
115~131 |
3.2.3具有高程抵偿面的任意带高斯正形投影平面直角坐标系
我们已经知道,影响长度变形的因素主要有两个,一是将实地距离化算至参考椭球面的变形,再者是将投影面上的长度投影至平面坐标的变形。前面所述的两种方法都是改变其中的一种长度变形而将综合变形控制在允许的范围之内的。而此种方法则同时改变了两种变形量,这也是一般工程中经常采用的建立独立坐标系的方法。
选择平均高程面做投影面,通过测区中心的子午线为中央子午线,按高斯投影计算的平面直角坐标的建立可以分成以下几步:
⑴.利用高斯投影正反算的方法 ,将国家点的平面坐标换算为大地坐标( B ,L );并由大地坐标计算这些点在选定的中央子午线投影带内的直角坐标( X ,Y ) 。关于高斯投影坐标的正反算问题在前面已经做了详细的介绍。
⑵.选择其中一个国家点作为“原点” ,保持该点在选定的投影带内的坐标设为(![]() ,
,![]() )不变,其他的国家控制点可以换算到选定的坐标系中去,公式为:
)不变,其他的国家控制点可以换算到选定的坐标系中去,公式为:
![]()
![]()
(把选定的坐标系中的点换算到国家坐标系统时亦采用此公式)
经过换算后的各国家控制点可以作为新建立的独立坐标系里的控制点,作为控制网的起算数据。
这种方法是将测区的平均高程面作为投影面,测区的中心子午线为中央子午线,是综和前两种坐标系统的优点的一种任意高斯投影计算平面直角坐标系,是工程单位常用的测量坐标系统。
3.2.4独立平面直角坐标系
这是当测区控制面积较小,不可进行方向和距离改正,直接把局部地球表面作为平面而建立的独立平面直角坐标系。这种坐标系可与国家控制网联系,取得起始坐标及起始方位角;亦可采用假定坐标。公路勘测规范规定,三级(含三级)以下公路、独立桥梁、隧道及其他构造物等小测区方可采用。
3.2.5计算新椭球常数
在工程应用中,当采用独立坐标系统时往往需要改变高程归化面而使综合长度变形控制在允许的精度范围之内,这样做的话就会使新的投影面与国家参考椭球面不一致,在进行坐标计算时由于椭球常数发生改变而使坐标计算存在误差,因此必须计算新的椭球常数。
新椭球常数按下列方法和步骤进行。
(1)新椭球是在国家坐标系的参考椭球上扩大形成的,它的扁率应与国家坐标系参考椭球的扁率相等。
即
![]()
第一偏心率和第二偏心率也与国家参考椭球相同;
即
![]()
(2)计算该坐标系中央地区的新椭球平均曲率半径和新椭球长半轴:
新椭球平均曲率半径为:
![]()
![]() 式中:
式中:
![]() 为该地区平均大地高;
为该地区平均大地高;
α为国家参考椭球长半轴;
![]() 为城市中心地区的平均纬度。
为城市中心地区的平均纬度。
新椭球的长半轴按下式计算:
![]()
(3)计算新椭球常数。
新椭球确定后,全部计算工作都要在新椭球面上或者通过新椭球传算到高斯平面上进行。而其中进行的大地坐标的正反算工作是大量的。1997年《测绘通报》第3起登载了中国测绘科学研究院顾旦生研究员的“一组高精度椭球面电子计算实用公式”文章,其中有一部分列出了大地坐标正反算公式的全部内容,但涉及很多椭球常数,只有计算出这些新椭球常数,这组公式才能在地方独立坐标系中得以应用。现将这些椭球常数的计算公式列出以供参考:
![]() ,
,
![]()
![]()
![]()
![]() ),
),
![]()
其中:
![]() ),
),
![]() ),
),
![]() ),
),
![]()
![]()
![]()
另一组常数为:
![]()
![]()
![]()
![]()
![]()
新椭球常数计算后就可以将属于国家大地坐标系的起算点转换为地方独立坐标系。
设某起算点在国家坐标系中的大地坐标为B,L,由于新椭球的球心与旧椭球重合,扁率不变,经度不会发生变化,
即
![]()
其纬度值为:
![]()
![]()
式中:
![]()
![]()
Δa为两椭球的长半轴之差,
![]() 为国家参考椭球第一偏心率
为国家参考椭球第一偏心率
再根据新布设的中央子午线,采用高斯投影正算公式可将![]() 、
、![]() 化为
化为![]() 、
、![]() ,然后对所有观测数据均以新坐标系为准进行化算和平差。如果要将独立坐标系点的坐标化为国家坐标系,只要根据高斯投影反算公式计算出
,然后对所有观测数据均以新坐标系为准进行化算和平差。如果要将独立坐标系点的坐标化为国家坐标系,只要根据高斯投影反算公式计算出![]() 、
、![]() , 然后利用上列公式化为国家坐标系的
, 然后利用上列公式化为国家坐标系的![]() ,再利用高斯投影正算公式并根据国家坐标系相应的中央子午线,即可化为
,再利用高斯投影正算公式并根据国家坐标系相应的中央子午线,即可化为![]() 。
。
3.3.1测区任意一点高差h 的最大允许值
为使投影改正达到应有的精度,必须分析h最大允许值。以下计算取S= 1 km,d =![]() 25 mm 。
25 mm 。
设测区任一点与平均高程的高差允许值![]()
由式![]()
![]() 可以写成
可以写成 ![]()
若取![]() 的极限值
的极限值![]() 25 mm/km ,可得
25 mm/km ,可得![]() =
=![]() 159 m ,由于极限值
159 m ,由于极限值 ![]() 25 mm/km是
25 mm/km是![]() 和
和![]() 两项改正之和的允许值,因此
两项改正之和的允许值,因此
![]()
(其中![]() 和
和![]() 的公式在本章第一节中已作推导)
的公式在本章第一节中已作推导)
3.3.2测区东西任一向长度的最大允许值y
根据中央子午线在测区中的位置不同可分为两方面进行讨论,即中央子午线过测区中心时高斯平面的投影改正和中央子午线在任意位置时在高斯投影平面上的投影改正。
3.3.2. 1中央子午线过测区中心时高斯平面的投影改正变化值
当中央子午线过测区中心时![]() = 0 ,则由计算公式
= 0 ,则由计算公式![]() 可得y与
可得y与![]() 的变化值,从而得知:
的变化值,从而得知:
当中央子午线经过测区中心时,即使测区范围很大,高斯平面的投影改正也很小(远小于限差25 mm)。这就是很多实际工程测量人员在采用抵偿高程面建立独立坐标系时将高斯投影改正视作常数而对其变化量不予考虑的原因所在。
3.3.2. 2中央子午线在任意位置时的![]() 值
值
将计算![]() 的公式
的公式![]()
![]() 可以改写成以下形式
可以改写成以下形式
![]()
令 ![]() ,可得:
,可得:
![]()
若取![]() 的极限值
的极限值![]() 25 mm/km,则
25 mm/km,则![]() km 。由上式可以计算在不同的
km 。由上式可以计算在不同的![]() 值时
值时![]() 的允许值。
的允许值。
由以上分析可以得知:
⑴在不考虑投影至椭球面的改正的情况下,当中央子午线经过测区中心时,测区东西范围的长度可允许值可达到90 km 。
⑵在有改正变化允许值![]() 和
和![]() 值时,测区中心至东西一翼的允许长度是不一致的,
值时,测区中心至东西一翼的允许长度是不一致的,![]() 越小,其差值就越大。因此,在用抵偿面作投影面时,当测区的范围大小和高差变化使得变形总量接近极限时,可不以测区中心的y值作
越小,其差值就越大。因此,在用抵偿面作投影面时,当测区的范围大小和高差变化使得变形总量接近极限时,可不以测区中心的y值作![]() 值而作适当的调整以满足要求。
值而作适当的调整以满足要求。
⑶随着中央子午线与测区中心的距离的增大,测区东西一向的允许长度迅速减小。![]() 带横坐标自然值最大约160 km ,即在
带横坐标自然值最大约160 km ,即在![]() 带的边缘地区,测区东西方向一向长度若超过了6.2 km,高斯平面投影的改正变化量就已经超过了25mm,即使整个测区地形平坦,以测区地面作投影面,其总的投影改正值也已超过限差要求。这就是用抵偿高程面作投影面时应仔细考虑的地方。
带的边缘地区,测区东西方向一向长度若超过了6.2 km,高斯平面投影的改正变化量就已经超过了25mm,即使整个测区地形平坦,以测区地面作投影面,其总的投影改正值也已超过限差要求。这就是用抵偿高程面作投影面时应仔细考虑的地方。
若再考虑大地水准面改正的变化量![]() ,则:
,则:
![]()
![]()
若测区边缘高于测区平均高程的高差达到了100 m,测区的中心横坐标值为150 km ,则![]() =15.7 mm ,可得:
=15.7 mm ,可得:![]() =2.5 km ,这对测区的范围要求是非常严格的,因此,在山区测量时应特别注意。
=2.5 km ,这对测区的范围要求是非常严格的,因此,在山区测量时应特别注意。
3.3.3坐标系统最佳位置分析
在建立独立坐标系统,选择中央子午线和投影面的位置时,只需计算测区中任一点的两项投影改正之和不超过1:40000的精度要求即可,即:
![]() 25 mm/km
25 mm/km
式中:![]() 为k点的在独立坐标系统中的坐标自然值,
为k点的在独立坐标系统中的坐标自然值,![]() 为k点在独立坐标系统中的高程。然而,在实际工作中如此考虑不现实,应该根据具体情况作具体分析,其方法如下
为k点在独立坐标系统中的高程。然而,在实际工作中如此考虑不现实,应该根据具体情况作具体分析,其方法如下
3.3.3. 1在实际工程中如何确定中央子午线的位置
一般来说在允许的情况下,采用抵偿高程面建立坐标系统是一种简便实用的方法。但在测区距中央子午线较远,测区范围或地形起伏比较大时,能否采用抵偿高程面作投影面的方法就需要进行仔细的分析和准确的计算了。根据以上分析可知,如果采用一个坐标系能覆盖整个测区的话,将中央子午线设在测区中心应该是最合适的解决方法。
3.3.3. 2如何确定最佳投影面位置
将中央子午线设在测区中心后,还需考虑投影面的位置。当测区地形起伏较大而相对范围较小的地区,将投影面设在测区的平均高程面上是一种比较好的方法。
对于地形平坦或高低起伏较小而范围相对较大的测区,取平均高程面作投影面也不是理想的选择,尤其是测区范围达到了极限(如平原地区的大型线路工程)的测区。选择最佳投影面位置的基本方法是:
由于高斯平面投影始终为正值,中央子午线设在测区中心,则高斯平面投影改正最小值就在测区中心,其值为0 。这时应考虑将投影面尽可能的下移使在椭球面上投影改正为负值以尽可能的控制最大的测区范围。具体要求是:
⑴测区中心处的参考椭球面投影改正值不超过其允许值![]() ;
;
⑵测区边缘两项改正之和不超过其允许值d。
设测区中心地区的高程为![]() ,测区边缘与中心处的高差为
,测区边缘与中心处的高差为![]() ,当整个测区地形条件允许时,投影面的最佳位置为 H =
,当整个测区地形条件允许时,投影面的最佳位置为 H =![]() -159 m 。
-159 m 。
测区边缘的大地水准面投影改正为:![]() ,
,
两项改正之和为:![]() ,
,
取![]() 25mm/km ,S = 1 km ,可得:
25mm/km ,S = 1 km ,可得:
![]()
当测区地形平坦的时,![]() = 0 ,则
= 0 ,则![]() =63 km 。这样尽可能的加大测区范围,对于大型线状工程测量工作具有实际应用价值。
=63 km 。这样尽可能的加大测区范围,对于大型线状工程测量工作具有实际应用价值。
4 小结
线路独立坐标系主要是针对线路工程建立的坐标系统。由于线路工程一般跨度比较大,当采用国家统一坐标系统时,往往会因为投影长度变形超限而不能满足工程需要,这时就需要考虑建立独立坐标系统。
独立坐标系统的建立主要考虑的是如何使高斯投影长度变形控制在允许的精度范围之内,从而达到精度要求,这时就需要对抵偿高程面的最佳位置以及中央子午线的最佳位置进行分析讨论。当采用抵偿高程面作投影面建立独立坐标系统时,不但要考虑测区距中央子午线的位置和测区的平均高程还要仔细分析测区的高低起伏情况以及测区的大小。当以测区中心为中央子午线建立独立坐标系统时应尽可能地下移投影面的位置,从而使测区范围尽可能地扩大。
当线路由于过长而跨越几个投影带时,采用一个坐标系统就不能满足工程需要,这时就需要建立多个坐标系统,并且要进行相邻投影带之间的换带计算以达到多个坐标系统之间的统一。
参考文献
[1]张凤举,张华海,赵长胜,孟鲁闽,卢秀山编著.控制测量学.北京:煤炭工业出版社,1999
[2]聂让编著.高等级公路控制测量. 北京:人民交通出版社,2001
[3] 高井祥,张书毕,汪应宏,张绍良,张华海编.测量学.北京:中国矿业大学出版社,1998
[4]王继刚,王坚,于先文.具有抵偿面的任意带高斯投影直角坐标系的选取方法.测绘通报,2002,(11)
[5]刘长星.建立独立坐标系统的研究.测绘技术装备,2002,(1)
[6]施一民,李健,周拥军,张文卿.地方独立坐标系的性质与区域性椭球面的确定.测绘通报,2001,(9)
[7]孔祥元,梅是义主编.控制测量学:(下册)[M].武汉:武汉测绘科技大学出版社,1996
[8]中孝顺,聂让编著.测量学.北京:人民交通出版社,1997
[10]陈士银.建立地方独立坐标系的方法.测绘通报,1997,(10)






