CAD可以更轻松地解决最严峻的设计挑战,借助其自由形状设计工具能创建所想像的形状。CAD的应用范围广泛,所以有时候我们会需要制作半球体,那么CAD怎么计算北半球纬度?利用直尺圆规即可做到,一起看看吧!
第1步
首先记住一个常识,在北半球,地表不同地点的地理纬度,实际上是这个地点到地球中心连线与赤道平面夹角的度数。这个度数与当地北极星的仰角度数是相等的。因此可以通过测量当地北极星的仰角高度,确定当地的地理纬度 。北极星的仰角就近似等于当地的纬度值。但因为北极星不严格在北极点,所以用测量北极星仰角得纬度会有大约半度的误差。
第2步
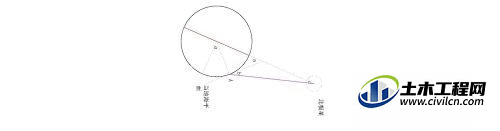
根据上图,可以很容易的理解,纬度a=仰角b+c。距有关资料,北极星与地球的距离以光年计,约400光年,而地球半径才不过6400km以下,两者相差太远,角c近视等于0。这其实也是为什么在天体中光线基本上是按照平行线来处理的。因为天体距离动辄以光年计,与星体自身的半径相差过大,星体上不同点位的视角几无差别。可视为平行线。
第3步
然后可以根据本系列经验4,(CAD与直尺圆规高级应用:[4]制作简易量角器)制作简易量角器。
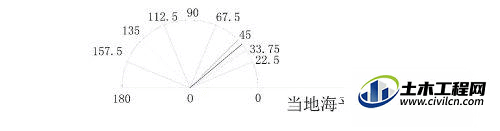
第4步
然后使量角器的0度线与海平面平行

第5步
然后在量角器上放上直尺,找一个视线较好能看见北极星的地点。

第6步
保证直尺的一段在量角器中心零点,另一端则指向北极星。注意需要同时保证量角器的0-0度与海平面一致未被移动。将直尺固定并在量角器上划线,估算其角度。此角度加减半度即为当地纬度。

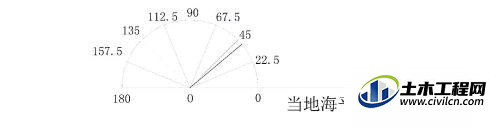
第7步
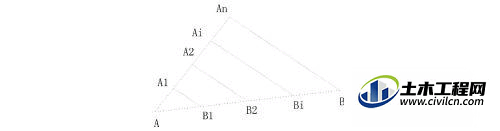
当量角器精度不够时,再采用本系列经验2,(CAD与直尺圆规高级应用:[2]如何将一个角平分),将包含北极星仰角的最小量度角再平分。可初步估计示例当地纬度在39.375在45度之间,并且非常接近39.375度。(示例实际为40度)